编译原理

一. 词法分析

词法分析就是将输入的字符流,分解成一个个的单词,并且对每个单词进行归类.

1) token

书中首先介绍了token这一种基本的单位,并且举了几个代码段,来进行说明,其中token常见的几种类型有这些.

image-20221007125140226

对于一段代码如下,经过词法分析器之后可以产生如下的效果:

image-20221007125224262

2) 正则

但是如何从文本(字符序列)解析出一个个的token呢?首先需要介绍的是正则表达式这一形式化的表达方式.正则表达式可以定义某种字符串的格式,对于输入的字符串可以进行匹配,根据是否匹配的结果可以确定给定的字符串是否符合某种类型.关于正则表达式的一些语法上的细节就不再多说.

在此还是提几个需要注意的细节吧,星号(*)即可重复,表示的是0个或多个.关于“|”则表示必选其一的或.

下面有几个例子:

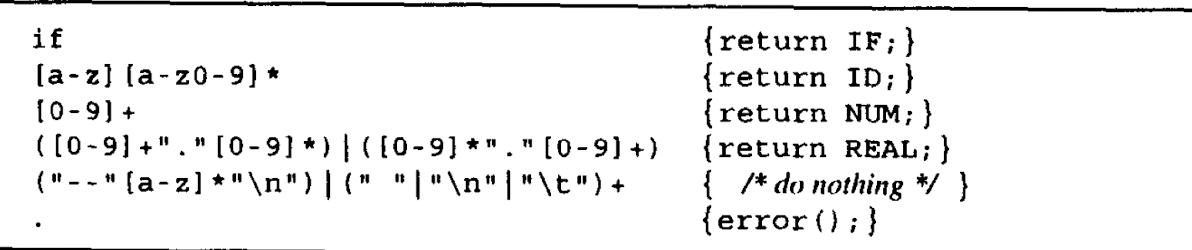
image-20221007130055006

还有正则匹配的二义性问题是需要注意的,比如说if8.处理方法有:

  • 最长匹配,由于一个字符串可以匹配出多种类型的正则,那么选取其中最长的一种正则类型.(在这里if8就是identifier,虽然也可以匹配到IF关键字和8但是不是最长的).
  • 规则优先,第一匹配完的正则有效.(if8结果为if).

但是仅仅是依赖正则表达式还是不够的,正则表达式只能匹配出字符串的类型,但是我们还需要做什么呢?

一般情况下,词法分析器的作用是用来分析最长匹配.

3) 自动机

我们需要以一种编程模型来实现正则表达式.所以也就提出了有限自动机的概念.

在词法分析的有限自动机中,每个边上的条件对应正则表达式上的一位字符.在运行时,一个字符串将会逐个字符的输入自动机,最终达到终态的就可以接受,如果到达某个非法状态,或者走投无路了,则拒绝该字符串.

对于某个字符串对一个有穷自动机不匹配的情况:当字符输入完了,但是还没有到达状态机final state;或者中间某个状态无边可选.

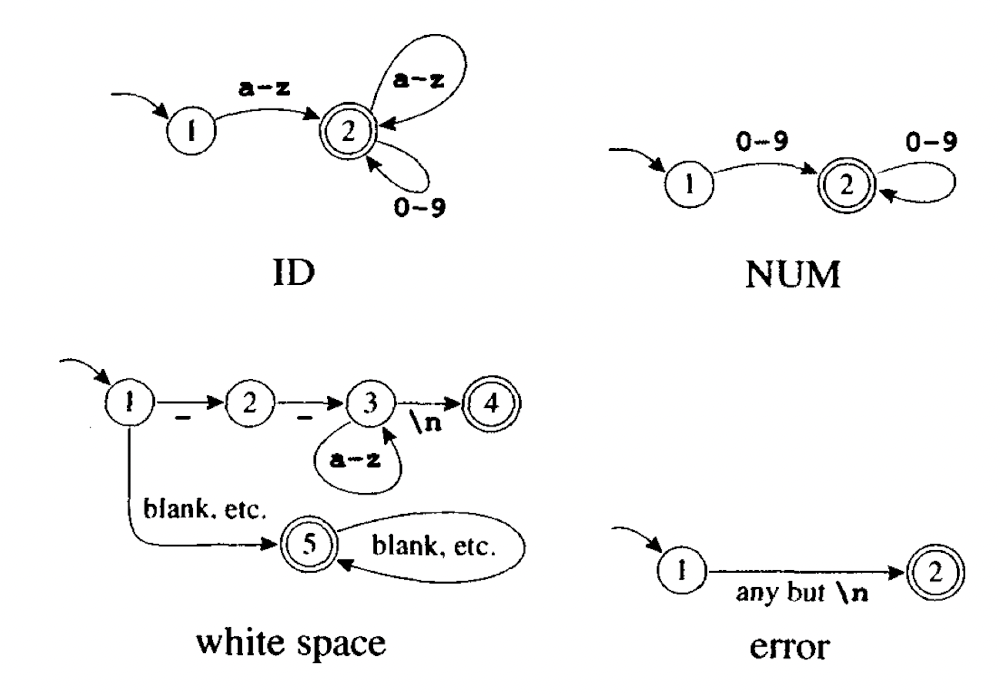
image-20221007131031745

至此,我们可以根据各种类型的正则表达式得出各自的自动机,但是真正使用时需要一个合并的大的自动机,并且又穷自动机还可以表示成矩阵的形式:

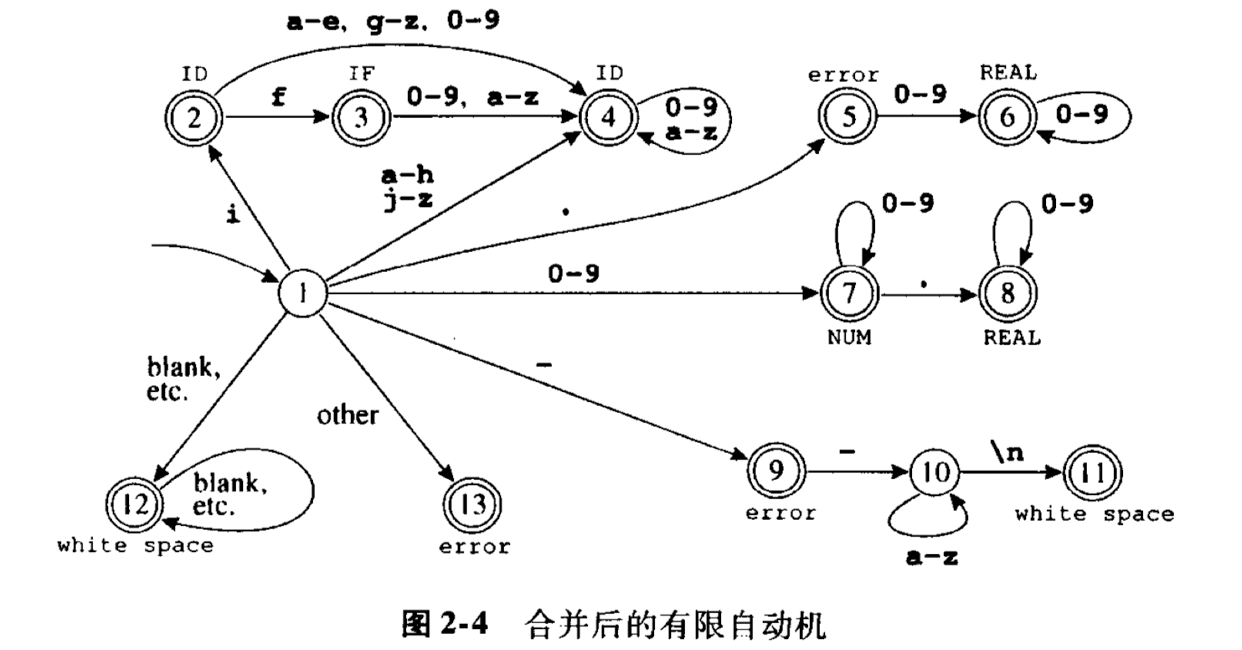
image-20221007131326733

在使用自动机进行字符串匹配的过程中,需要记录最长匹配的位置和长度.因此会有两个变量被维护(Last_Final,Input_Position_at_Last_Final).

既然有了一般的自动机,还要NFA有何用呢?其最大的特点在于非确定,每走一步可以尝试不同的分支(同一个符号).这也可以用来实现正则表达式.

这一部分的难点在于正则到NFA和NFA到DFA的转换.

正则转NFA

首先我们需要明确在正则语法中:**|,·,*是基本的联结运算符号**,因此任何正则表达式都可以转换为只有这3中符号的表达方式,而根据这几种连接符号的性质,我们很容易得出其NFA的表达形式:

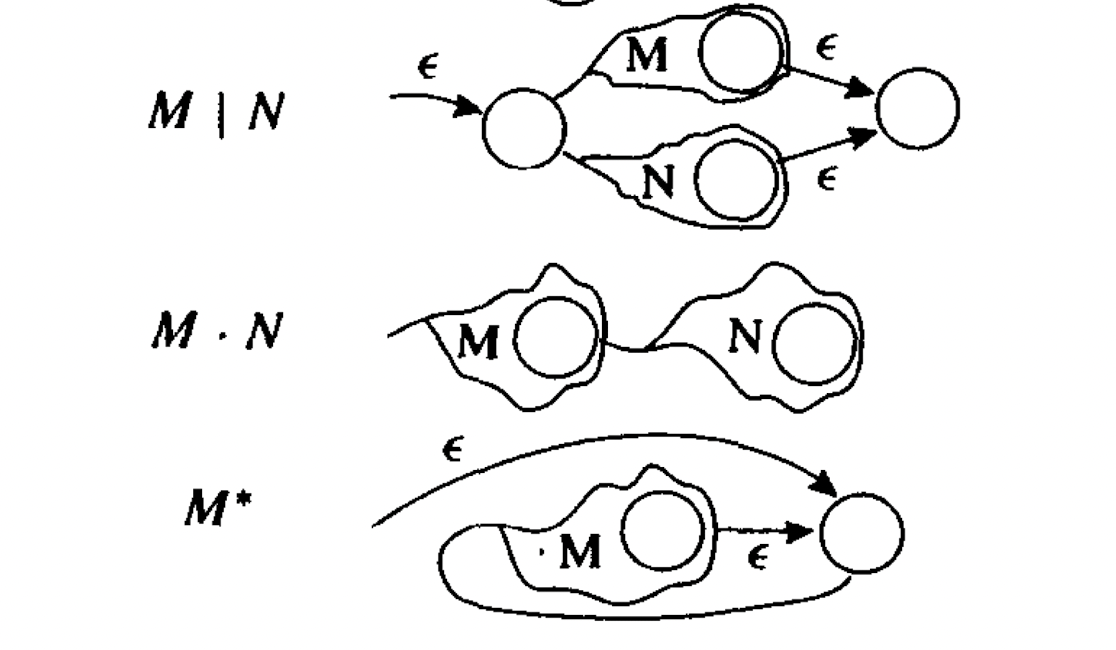
image-20221104220138064

所以可以将M,N递归地转换成NFA的形式,最终也就可以得到NFA的表达形式.

NFA转DFA

这一部分相对来说要复杂一些.

书上讲得太抽象了,找了篇博客感觉写得挺好:NFA到DFA的转化(保证能讲明白),然后在找几个例子动手写一写,大概就可以理解是怎么一回事了.

最小化DFA

lex是构造词法分析器的强力工具,其输出是一个c语言文件,即根据我们的定义生成的词法分析模块的程序代码.

二. 语法分析

语法是将单词组合成词组,从句或者句子的方法.

0. 语法表示的困难

比如说,我们既然可以将字符以正则的语法组成一个表达式,那么如果我们是不是就可以考虑用一个由token组成的表达式就好了?比如说

digits = [0-9]+
sum = (digits "+")*digits

对于上面的方式,直接将表达式进行代换就可以得到sum的结果,一个由正则表达式组成的式子.

但是一些表达式的代换需要考虑递归的问题.比如说:

digits = [0-9]+
sum = expr "+" expr
expr = "(" sum ")" | digits

如果考虑直接对sum进行,直接考虑将sum进行代换的话,就会导致无休止的递归问题.

1. 上下文无关文法

上下文无关文法是一个产生式的集合,还包括一些列开始符,终结符,非终结符等.每个产生式的格式如下:

symbol -> symbol symbol ... symbol

举几个例子:

S -> aSb
S -> ab

我们将最左边的S成为非终结符,我们只要找到了符合右边的串,就可以将其归为S.结合书上的例子:

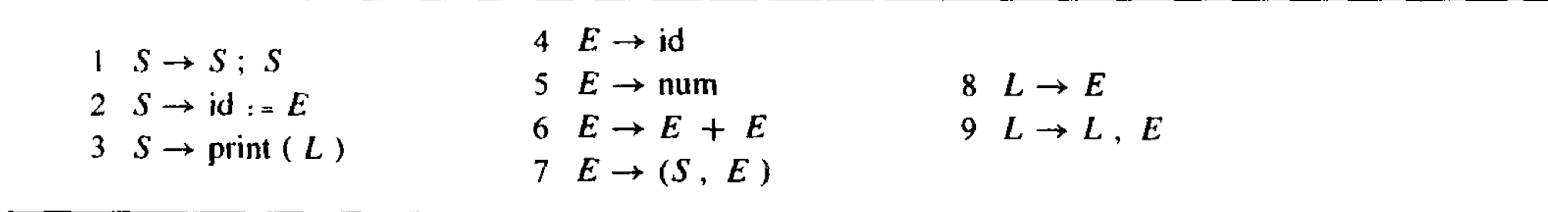
image-20221112152742227

以上产生式的集合就可以表示一个文法.终结符是一个产生式中,不可继续分解的最小单位符号.比如上面的num,id,+等等.可以继续分解的就是非终结符.

关于语法的推导,指的是将一个开始符号,对于其右部的每一个非终结符,都用此非终结符产生式中的任意一个右部进行替换,递归地进行,直到无法再进行替换为止,最终所有非终结符将会消失,推导有分为最右推导和最左推导.如下所示:

image-20221112153605011

关于推导的过程,可以将推导的过程组织成一个语法树.此外,很多文法其实可以最终推导成不同的形式(语法树),称之为二义性语法.对于语法二义性应当是我们要避免的东西,因此有一些文法转换的方式.常见的方法有:增加一些非形式化的定义或者设计无二义性的文法.

文件结束符

文件结束标志往往也是语法分析器必须要读入的,比如说可以用\(表示.往往会额外引入一个开始符号S‘,多一个产生式S’ -> S\)

2) LL文法

首先我们需要了解的是,LL文法指的是什么?LL文法对应了语法树以先序遍历方式,即自顶向下.

需要明确的是LL文法分析的先决条件:

  • 消除左递归问题.
  • 解决回溯问题.

回溯与左递归问题

对于一个输入的字符串,从开始符号出发,不断地将非终结符进行替换,直到没有非终结符为止,最终建立起一个语法树.最终确定一个推导式.但是容易导致的问题有:

  • 在替换的时候,对于同一个非终结符有多种替换方式,并且这其中并非每种替换方式都正确,一旦递归到某地方后发现错误,就需要回溯,然后继续试探.这会带来较大时开销.
  • 左递归所导致的无限循环,如果某一个非终结符可替换的方案中,与该非终结符有共同的前缀,并且始终在递归中无法消除.

关于回溯问题的处理,简而言之,本质是因为某一个非终结符的多个产生式中,具有公共左因子,因此在制定文法时,需要保证每个非终结符的多个产生式之间不可以有公共左因子.因此可以采用提取左因子的方法,如下:

image-20221112164636369

关于左递归问题的解决.这种现象分为直接左递归和间接左递归.定义如下:

直接左递归 文法G中有形如A->Aa的产生式
间接左递归 文法G中无形如A->Aa的产生式,但是可以经过有限步骤得到A->Aa

关于直接左递归的消除:

  • 以产生式中无左递归的部分为前缀,生成右递归表达式.
  • 对于有左递归的部分,去除公共前缀,之后写成右递归的形式(末尾还有一个空符).

image-20221112165658377

至于间接左递归的消除方法,首先通过代换的方式,转换成直接左递归问题,然后按照直接左递归进行处理即可.

First和Follow

首先需要了解两个定义:

  • First(a),a是一个给定的符号串,First就是该符号串中的首终结符集合.
  • Follow(A),是对于非终结符的在整个文法中的后随(紧接的)终结符号的集合.

其中对于给定的非终结符A,如何计算其follow集合,需要扫描每个含有A的产生式,描述算法如下:

image-20221113181438586

知道Follow大小不再扩张时,Follow构造结束.

其实对于LL文法先决条件的描述,通过Follow和First进行更精确的描述如下,如果满足这些条件,也就说明没有左递归与回溯:

image-20221112174031613

因此,我们需要先求出Follow和First,然后判断是否符合LL的条件.

预测分析表的构建

下面主要涉及到LL(1)文法有关的部分,LL(1)文法是一种不需要回溯的自顶向下算法.

至此,我们考虑两个问题.一个是,如何构建预测分析表,并且构建出来之后,该预测分析表又是怎么用的呢?关于预测分析表,结构如下:

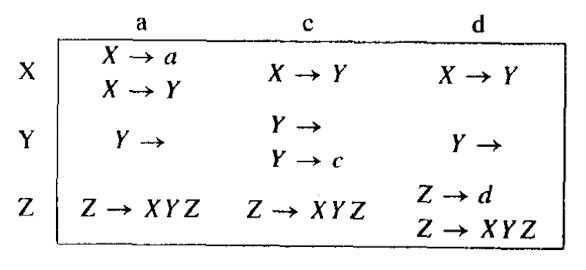
image-20221112180019132

每一行对应一个非终结符,每一列对应所有终结符.因此通过检查每个产生式,填表即可.可以参考这个例子编译原理LL(1)预测分析表的构造.

描述算法如下:

image-20221113182522005

然而预测分析表是怎样在递归下降中使用呢?

这篇文章中对于parsing的过程有很详细的推导:编译原理语法分析之LL(1) parser

推导就是一个伴随着字符串的输入而进行入栈和弹栈的过程,每一步入栈对应了一个非终结符的转化,这里转化的过程是根据预测分析表决策的.

3) LR文法

LR(k)分析代表的是,从左到右分析,最右推导,超前查看k个单词.

image-20221112195012284

从此图可知,相比LL(1)文法每次查看一个符号就根据预测分析表来对战进行规约或压入,LR文法则是先将符号压入,如果符合规约的条件,再递归地进行规约动作,直到扫描到结束字符,而且此时栈中只有一个S.LR文法对应了语法分析树中的后序遍历.

除此之外,我们还可以发现,栈内的元素+输入缓冲区的内容总是等于一个”规范句型“.

LR语法分析算法

LR分析器是怎样知道如何移进或者规约的呢?答案是通过有限自动机来进行的.这种有限自动机是作用于栈的动作的.

其中如下所示:

image-20221112210515455

其中的纵坐标表示的是栈的状态,而横坐标表示的是当前要输入的符号.关于对于其中动作的说明:

  • sn表示的是移进,并且转换到状态n.
  • rk表示的是规约,根据文法中的规则k依次弹出单词(弹出单词的数量与产生式右半部分相同).然后压入产生式左半部.

因此我们的任务也就是,如何根据文法构建出这样的一个状态机.

image-20221113191618033

LR(0)分析器

三. 语义分析

1) 上下文有关文法

为什么需要进行语义分析呢?

  • 需要捕获一些Parser捕获不了的错误.Parser只能从形式上的错误进行捕获(正所谓上下文无关文法).而一些语义上的错误却捕获不了(这种语义上的错误可以认为是上下文有关文法),因此还涉及到类型检查等工作.
  • 对于程序中的Identifiers需要补充一些额外的信息(即符号表).这在具体的实现上体现为符号表的构造及其Bindings的设置.

然而关于一些语义上的问题,具体都是指什么呢?

  • 类型不匹配.
  • class继承问题.
  • 重复定义问题等等.

还有许多不再一一枚举,这些都是与某个语言的具体定义有关的,其本质上也就是上下文有关文法.

2) 基本概念

接下来简要说明几个核心的概念:符号表,绑定,作用域.

绑定是对于每个Identifier名及其相关信息所组成的数据结构,也就是符号表中的条目.一个Identifier最基本的信息就是类型(究竟是函数,还是变量,还是对象,对于同一种类型的Identifier还可以再往下区分类型,比如说int还是string等等),一般在实现时对于不同的Identifier会有不同类型的绑定,其中的字段也有所不同,比如说对于一个函数类型的绑定中往往会有参数,返回值等等.还有其他比较必要的信息,比如size.

符号表是绑定的集合,一个符号表可以采用不同的数据结构来存储,比如说散列表等等,数据结构的选择是一个重要的问题.符号表在实现时往往会又一些增,删,查相关的接口.

作用域也是和符号表息息相关的,因为绑定的有效性(也就是一个Identifier的生命周期往往是和作用域有关的),比如说当遇到某个变量的声明时,首先将其加入到当前作用域的符号表中,当离开该作用域时,就需要将该Identifier移除,很多Identifier遵循的是“先声明后引用”的原则,因此当对某个Identifier进行处理时都遵循从最近作用域向外部查找的方式.而对于一些语言中的class定义就不同(比如说cool),一般是不遵循“先声明后引用的原则”,因此其在处理上需要额外地先进行全局性地扫描.

3) 结合Tiger代码分析实现

虎书中介绍了一种基于散列表实现的符号表.

typedef struct TAB_table_ *S_table;
S_table S_empty(void); // 返回一个空的符号表
void S_enter(S_table t, S_symbol sym, void *value); // 将符号sym加入到当前作用域
void *S_look(S_table t, S_symbol sym);  // 从符号表t中查找符号Sym,
void S_beginScope(S_table t); // 进入当前作用域
void S_endScope(S_table t); // 离开当前作用域

其中符号表的具体定义如下:

typedef struct binder_ *binder;
struct binder_ {  
  void *key; 
  void *value; 
  binder next; 
  void *prevtop;
};
struct TAB_table_ {
  binder table[TABSIZE];
  void *top;
};

由此可见,TAB_table主要是一个散列表,数组table的每一项对应每一个链表.其中top指针适合维护作用域息息相关的变量,可以说为了实现作用域,还需要维护一个辅助栈,在后续详细说明.

此外还值得一提的是,符号表所接收的参数是S_symbol,这里本应该是一个表示Identifier的字符串,但是这里由于采用了散列,因此还需要实现与该散列相关的Hash函数,其中有关S_symbol的实现如下:

struct S_symbol_ {  
  string name; 
  S_symbol next;
};
#define SIZE 109  /* should be prime */
static S_symbol hashtable[SIZE];

因此我们可以得出这代表的是一个结点,其内容为一个Identifier的name.后面有一些与散列有关的实现.

接下来是一些符号表中的具体操作的实现:

void S_enter(S_table t, S_symbol sym, void *value) {
  TAB_enter(t,sym,value);
}
void *S_look(S_table t, S_symbol sym) {
  return TAB_look(t,sym);
}
static struct S_symbol_ marksym = {"<mark>",0};
void S_beginScope(S_table t) { 
  S_enter(t,&marksym,NULL);
}

void S_endScope(S_table t) {
  S_symbol s;
  do s=TAB_pop(t);
  while (s != &marksym);
}

其中enter是通过直接调用TAB_enter实现的,look同理,S_beginScope的实现是基于S_enter实现的,可以将其理解为向符号表加入一种特殊的符号,也就是<mark>,专门标记一层作用域.关于S_endScope也就是其逆操作,一直pop,直到遇到<mark>标记之外.

至此我们可以简单地推测在更底层的TAB相关的实现中,既要维护散列表,也要维护辅助栈.辅助栈的作用在于可以通过<mark>将入栈的一层层Identifier划分为不同层次的作用域.更多细节如下所示:

void TAB_enter(TAB_table t, void *key, void *value) {
  int index;
  assert(t && key);
  index = ((unsigned)key) % TABSIZE;
  t->table[index] = Binder(key, value,t->table[index], t->top);
  t->top = key;
}
void *TAB_look(TAB_table t, void *key){
  int index;
  binder b;
  assert(t && key);
  index=((unsigned)key) % TABSIZE;
  for(b=t->table[index]; b; b=b->next)
    if (b->key==key) return b->value;
  return NULL;
}

void *TAB_pop(TAB_table t) {
  void *k; binder b; int index;
  assert (t);
  k = t->top;
  assert (k);
  index = ((unsigned)k) % TABSIZE;
  b = t->table[index];
  assert(b);
  t->table[index] = b->next;
  t->top=b->prevtop;
  return b->key;
}

其中enter是获取该symbol的散列值之后,将其加入到散列表中,并且直接入栈.对于look来说,直接从散列表中查询即可,而对于pop来说,既要从辅助栈中弹出,也要从散列表中移除.

关于Binding中的具体信息,这些将会在types.h等文件中有所体现,也就对应了binder_中的value,由于使用了void*,因此可以实现一种类似于多态的机制:

struct Ty_ty_ {
	enum {
    	Ty_record, 
    	Ty_nil, 
    	Ty_int, 
    	Ty_string, 
    	Ty_array, 
    	Ty_name, 
    	Ty_void} kind;
	union {
    			Ty_fieldList record;
		      Ty_ty array;
		      struct {
            	S_symbol sym; 
            	Ty_ty ty;
          } name;
		    } u;
};

4) 类型检查

类型检查实际上是在遍历AST的过程中进行的.这个过程中需要更新和查看符号表.也就需要用到上面所介绍的接口.cs143的课程中还介绍到了类型检查有关的形式化表示,在此不再多说.在此主要叙述类型检查的实现.

四. 运行时环境与活动记录

1) 概述

​ 运行时环境以及活动记录的作用是什么呢?我们需要管理运行时资源(变量,对象等等),动态数据和静态数据,以及存储管理等等.当一个程序被载入到内存中时,其内存视图可以大致分为代码段和数据段,因此编译器有一个任务也就是生成代码段中的内容并且填充数据段.

​ 此外关于代码段中代码的执行,一般来说都是从某个点中开始进入,然后顺序执行指令,但是程序中都有像函数这样的过程抽象,如果想要实现“过程”这一概念,就不能只借助代码段中的顺序执行,因为过程的特点就是进入到一个函数后,结束后在恢复现场,因此就引入了程序动态内存区中的栈这一概念.栈是为了实现程序运行中的过程抽象.

​ 此外,代码段在程序中通常在建立之后就处于固定并且只读的状态,静态数据段中的变量都有着固定的地址(在程序初始化时就建立了,并且size通常也固定),栈和堆都处于动态的内存区之中,两者相冲增长,碰撞是应该避免的事情.

​ 关于栈这种数据结构,在之前的学习中已经非常熟悉了,在此只梳理一下栈帧.

2) 栈帧

3) Tiger中与栈帧相关的实现

五. 中间代码生成