mit 6.830 数据库系统: lab 3

yfs

2022-09-03

这一部分,只论练习的话不难,只用了一晚上+一上午就完成了,虽然也参考了一点别人的博客,毕竟执行与优化的很多工作已经给我们做好了,但是执行与优化这一部分还是非常复杂的.

1.总体架构

这个实验只需要只需要实现3个类,分别是直方图,table statistics还有JoinOptimiter.但是这并不意味着执行与优化的过程就这么简单.其基本的体系结构如下:

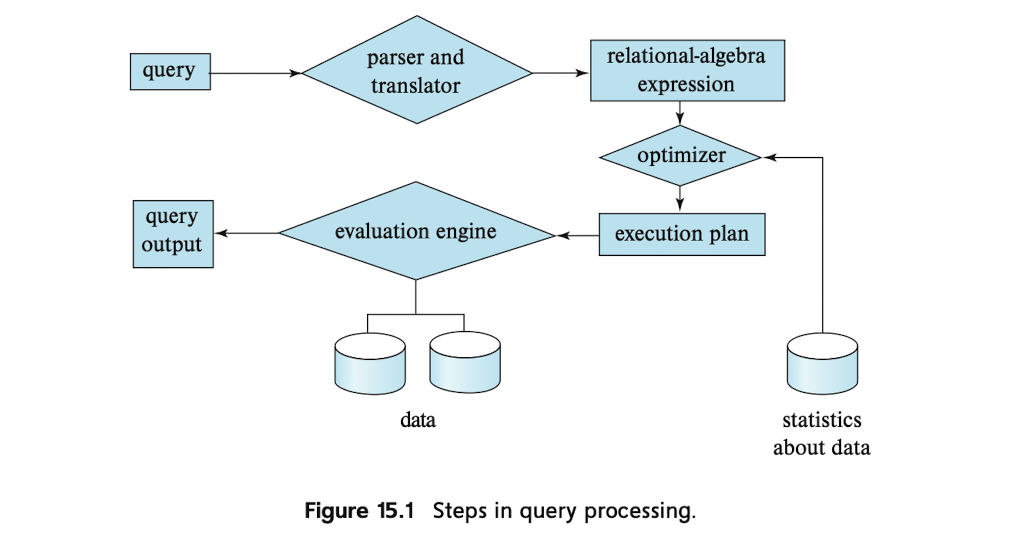
当数据库使用者使用query语句(比如说sql语句)发起查询时,经过sql解析器的作用,被翻译成了关系代数表达式的形式,此时生成的关系代数与保存的statistics作为共同输入到optimizer中,optimizer负责生成许多等价的表达式,并且为不同的表达式的开销进行评估并相互比较,最终选出一个最优plan执行.上述语言比较笼统,具体到SimpleDB中是这样的.

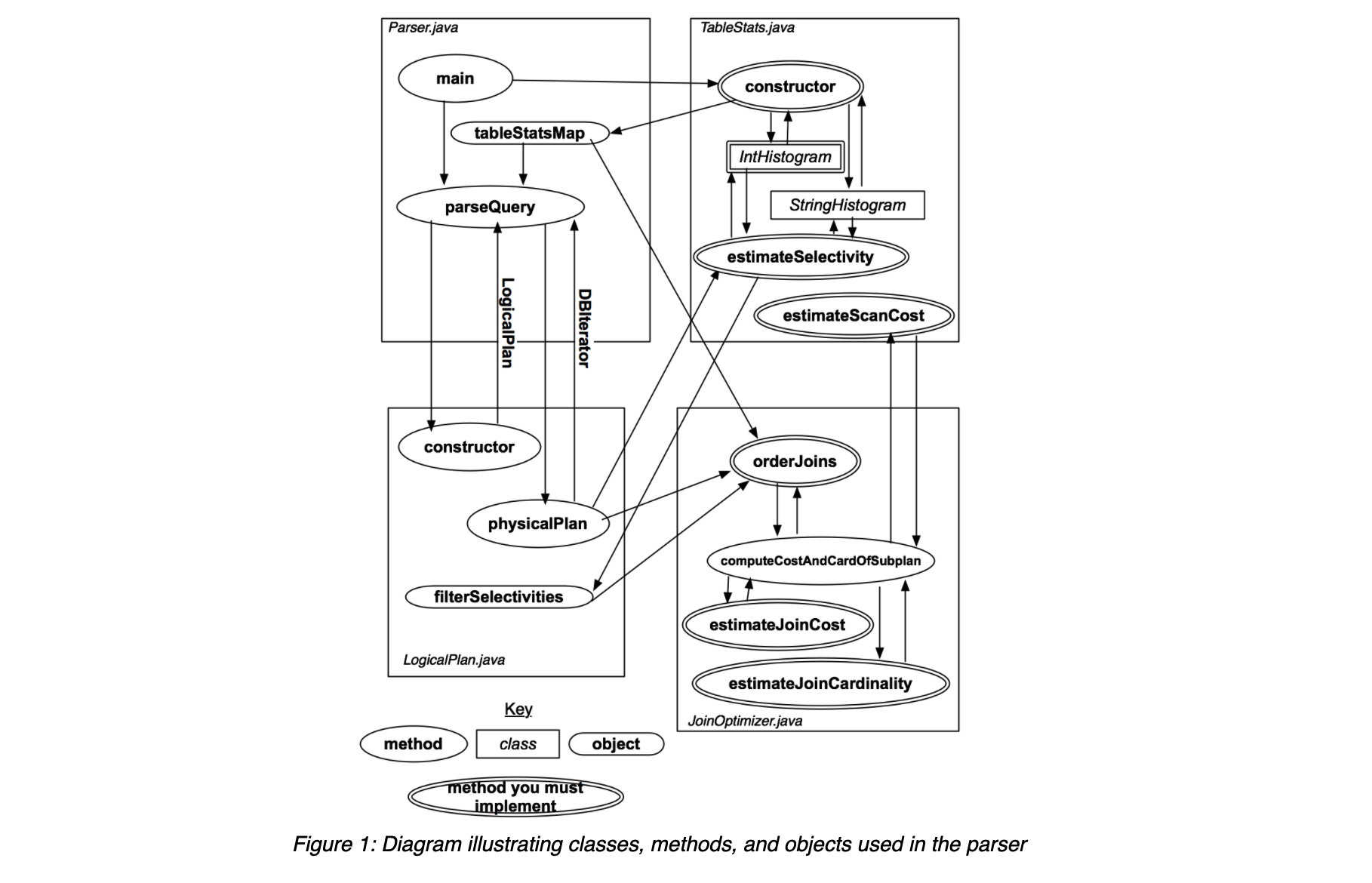
在这里,tableStatistics通常会在表add到catalog后,马上创建出tableStatis,这之后才会发生一些parse的行为.对于输入的sql语句,Parser.java中的parseQuery会讲语句翻译成LogicalPlan对象.一个LogicalPlan可以看作是一个操作序列,也可以用一个操作树来表示.

简述一下图中的执行流的话,在一个查询操作发起之前,假定该表及其statistic已经生成,再生成某个表的statistic时,也就是创建一个该表对应的TableStats对象,在该对象创建的时候,会对该表进行扫描,同事借助直方图对于表中的每个域中的数据信息进行统计,生成的TableStats会登记在一个全局的tableStatsMap中.

输入一个查询的sql语句后,调用parseQuery进行解析,在这个函数中,首先会创建一个LogicalPlan对象,然后调用该对象的physicalPlan函数,该函数会调用JoinOptimize的实现的最优顺序,最终返回生成的结果,其中DBIterator也就涉及到了在lab2中的东西.

2.实验过程

1) Exercise 1

这一部分的任务是完成直方图,难度不是太大,但是一些细节需要注意.

其中数据成员及构造函数如下:

private int bucketsNum_;
private int min_;
private int max_;
private Integer[] hightArray_;
private int nTups_;
public IntHistogram(int buckets, int min, int max) {
	// some code goes here
    bucketsNum_ = buckets;
    min_ = min;
    max_ = max;

    nTups_ = 0;

    hightArray_ = new Integer[bucketsNum_];
    Arrays.fill(hightArray_,0);
}

直方图的横轴是一个[min,max]的区间,会将将这个区间划分为bucketNum个range.estimateSelectivity实现如下,其中主要基于getLessSum这个函数.

public double estimateSelectivity(Predicate.Op op, int v) {
    String opStr = op.toString();
    double sum = 0;
	// some code goes here
    if (opStr.equals("=")) {
        sum = getLessSum(v + 1) - getLessSum(v);
    } else if (opStr.equals("<")) {
        sum = getLessSum(v);
    } else if (opStr.equals(">")) {
        sum = 1.0 - getLessSum(v + 1);
    } else if (opStr.equals("<=")) {
        sum = getLessSum(v + 1);
    } else if (opStr.equals(">=")) {
        sum = 1.0 - getLessSum(v);
    } else if (opStr.equals("<>")) {
        sum = 1.0 - getLessSum(v + 1) + getLessSum(v);
    }
    return sum;
}

getLessSum的函数实现如下,这个函数表示的是[min,v),也就是[min,v-1]在整个直方图中所占的贡献,首先对于超出[min,max]的部分进行特判,如果小于min则返回0,大于max则返回1.0.时候获取v所在的索引以及偏移量,然后遍历该index之前的所有range,并且进行累加,最后再加上根据offset得出v在其所在的range中所贡献的比重,最终返回结果.

private double getLessSum(int v) {
    if (v <= min_) {
        return 0;
    }
    if (v > max_) {
        return 1.0;
    }
    double sum = 0,width = getWidth(),offset = getOffset(v);
    int index = getIndex(v);
    for(int i = 0; i < index; i ++) {
        sum += (hightArray_[i] / (double) nTups_);
    }
    double cnt = hightArray_[index]/ (double) nTups_ / width;
    sum += cnt * offset;
    return sum;
}

关于index和offset的计算,实现如下:

private int getIndex(int value) {
    if (value <= min_) {
        return 0;
    }
    if (value >= max_) {
        return bucketsNum_ - 1;
    }
    double width = getWidth();
    int index = (int) ((value * 1.0  - min_) / width);
    return index;
}
private double getOffset(int value) {
    double width = getWidth();
    int index = getIndex(value);
    double offset = value - (min_ + index * width);
    return offset;
}

至于addValue的实现,首先特判v是否超出[min,max]的范围,否则直接返回,并不加入到直方图中,然后获取对应的index,并且将对应的index项+1.其他就没有什么好说的了.

2) Exercise 2

TableStats的实现是比较复杂的.其中数据成员如下:

private int tableId_;
private HeapFile tableFile_;
private TupleDesc tableDesc_;
private int ioCostPerPage_;
private int tupleNum_;
private HashMap<Integer,Field> maxValues_;
private HashMap<Integer,Field> minValues_;
private HashMap<Integer,IntHistogram> intHisMap_;
private HashMap<Integer,StringHistogram> strHisMap_;

TableStats是为每个表创建的有关于统计信息的数据结构,其中tupleNum表示这个表中的tuple的数量,maxValues_,minValues_,用来统计该Table中每个域的最大值和最小值,其中key代表的是一个field在表中的index.然后再初始化intHisMap_,strHisMap时,会根据已经设置好的maxValues_,minValues_进行设置.这些行为都发生在构造函数中,因此构造函数会涉及到对这个表的扫描,总的来说,会进行两次扫描.由于构造函数比较长,所以就不贴代码了,其过程如下:

设置tableId_,tableFile_,tableDesc_,ioCostPerPage_.
初始化maxValues_,minValues_.
扫描一遍tableFile_,每一个Page直接从File中读取,不使用BufferPool,没读取一个Tuple就对tupleNum加一,并更新maxValues_和minValues_.
然后根据minValues_,maxValues_的结果初始化intHisMap和strHisMap,再扫描一遍表,将每一个Tuple都加入到对应的直方图中.

由于这个过程中对整个表扫描了两遍,因此estimateScanCost的实现如下,其中需要乘2.0:

public double estimateScanCost() {
    double pageNum = tableFile_.numPages();
    return 2.0 * pageNum * ioCostPerPage_;
}

再estimateSelectivity,这个函数只要获取对应的直方图之后,调用该直方图中的estimateSelectivity即可.

public double estimateSelectivity(int field, Predicate.Op op, Field constant) {
    // some code goes here
    if (constant.getType().equals(Type.INT_TYPE)) {
        IntField intField = (IntField) constant;
        IntHistogram ih = intHisMap_.get(field);
        return ih.estimateSelectivity(op,intField.getValue());
    } else {
        StringField stringField = (StringField) constant;
        StringHistogram strh = strHisMap_.get(field);
        return strh.estimateSelectivity(op,stringField.getValue());
    }
}

关于estimateTableCardinality的实现更加简单.

public int estimateTableCardinality(double selectivityFactor) {
    return (int) (selectivityFactor * tupleNum_);
}

3) Exercise 3

练习3主要是对于一些估价方式的理解.代码量较小,只涉及到两个函数:

下面是estimateJoinCost函数,该函数用于返回一个Join节点的代价,其中参数card1和card2表示的是这个Join操作中两个Table中的Tuple的数量,cost1和cost2表示两个表的I/O代价,姑且不谈LogicalSubplanJoinNode分支情况,总的估价相当于一个cost1(需要扫描一遍table1)+ card1 * cost2(需要扫描card1遍table2) + card1 * card2(扫描时需要做断言判断所耗费的CPU).

public double estimateJoinCost(LogicalJoinNode j, int card1, int card2,
        double cost1, double cost2) {
    if (j instanceof LogicalSubplanJoinNode) {
        return card1 + cost1 + cost2;
    } else {
        double cost = cost1 + card1 * cost2 + card1 * card2;
        return cost;
    }
}

这也就对应了实验文档中的公式:

//p=t1 join t2 join ... tn
scancost(t1) + scancost(t2) + joincost(t1 join t2) +
scancost(t3) + joincost((t1 join t2) join t3) +
...

然后则是estimateTableJoinCardinality的实现,这个函数主要用于estimate两个表Join之后产生的Tuple的数量,这一部分的实现需要根据Predicate.op分情况讨论.

public static int estimateTableJoinCardinality(Predicate.Op joinOp,
                                               String table1Alias, String table2Alias, String field1PureName,
                                               String field2PureName, int card1, int card2, boolean t1pkey,
                                               boolean t2pkey, Map<String, TableStats> stats,
                                               Map<String, Integer> tableAliasToId) {
    int result = 0;
    if (joinOp.equals(Predicate.Op.EQUALS)) {
        if (!t1pkey && t2pkey) {
            result = card1;
        } else if (t1pkey && !t2pkey) {
            result = card2;
        } else {
            result = Integer.max(card1,card2);
        }
    } else {
        result = card1 * card2 * 3 / 10;
    }
    if (result <= 0) {
        result = 1;
    }
    return result;
}

对于EQUALS的情况,内部还需要根据主键的情况来进行讨论,如果至于一方是主键,那么其返回的元组数不会超出非主键的元组数,比如说table1有主键,而table2没有,那么其返回的结果就不会大于card2,最终返回table2.而对于两方都是主键或者都不是主键的情况,则返回max(card1,card2).关于不是EQUALS的情况,也就是范围扫描的情况,这里只做了一个粗略的估计,取两者乘积的30%.此外,如果其中的结果小于等于0,那么就返回1.

4) Exercise 4

这里主要实现一个用于选出最优顺序的动态规划算法,这个算法在这里就跟求最长单调序列的问题很像.

其中该算法的描述如下(该图来自《数据库系统概念第六版》):

该算法的原理在于,根据长度长短,由短到长地遍历子集,长子集的结果可以根据短子集的结果递推得出,对于某个S子集,可以有若干个划分为两段的方式,S子集中的最低开销方式一定就是其中之一,在这里也就是其中最低开销的划分方式,而每种方式中,都是P1.cost + P2.cost + A的代价,而P1和P2是短于S的子集,在此之前就已经推导出结果,因此可以直接利用.以此类推,直到递推到整个长度的序列,这种算法利用了Join操作作为二元操作可结合的特点,也利用了开销累加的计算方式.总的来说,与其说是给一连串的Join操作排序,不如说是如何利用结合律个这个表达式加括号(只不过这个括号也是有优先级之分的,包含的table越少的括号,优先级越高)进而得出最低开销的方式.

根据此算法,实现代码如下:

public List<LogicalJoinNode> orderJoins(Map<String, TableStats> stats,Map<String, Double> filterSelectivities, boolean explain)
         throws ParsingException {
     int n = joins.size();
     PlanCache planCache = new PlanCache();
     for (int i = 1; i <= n; i ++) {//从长度为1到长度为n
         Set<Set<LogicalJoinNode>> subsets = enumerateSubsets(joins,i);
         Iterator<Set<LogicalJoinNode>> subsetIt = subsets.iterator();
         while (subsetIt.hasNext()){ //内部分别对应一段集合
             //构造集合
             double optcost = Double.MAX_VALUE;
             List<LogicalJoinNode> bestList = null;
             int card = 0;
             Set<LogicalJoinNode> nodeSet = subsetIt.next();
             Iterator<LogicalJoinNode> setIt = nodeSet.iterator();
             while (setIt.hasNext()) {
                 LogicalJoinNode node = setIt.next();
                 CostCard csa = computeCostAndCardOfSubplan(stats,filterSelectivities,node,nodeSet,optcost,planCache);
                 if (csa != null ) {
                     optcost = csa.cost;
                     bestList = csa.plan;
                     card = csa.card;
                 }
             }
             planCache.addPlan(nodeSet,optcost,card,bestList);
         }
     }
     Set<LogicalJoinNode> allSet = enumerateSubsets(joins,n).iterator().next();
     List<LogicalJoinNode> resultList = planCache.getOrder(allSet);
     if (explain) {
         printJoins(resultList,planCache,stats,filterSelectivities);
     }
     return resultList;
 }

简单地说明一下实现,最外层for表示的是,从1到n的遍历,这也是整个动态规划算法的线索,也就是由短到长.在每一个长度对应的循环中首先借助enumerateSubsets来生成一个个在该长度下的子集.然后对这些子集进行遍历,每个子集都对每一种划分方式求解开销,通过computeCostAndCardOfSubplan来实现,然后对结果进行更新,当对一个子集的所有划分方式都尝试完后,就addPlan,表示该子集的下的最优plan已经保存好了,这可以在后来的递推中直接使用.当所有长度的都递推完后,最终长度为n的,就是最优解.

3.小结

做了这个lab,也对数据库执行与优化的整体框架有了初步的认识吧,此外也温习了一下好久没碰的动态规划算法.