mit 6.830 数据库系统: lab 5
1.实现基础
1) 索引系统
之前的lab中,Tuple在文件中的分布是没有规律的,而且想要在表对应的文件中查询一个Tuple,不得不在该文件中逐页地遍历查找,至于删除,插入等操作亦复如是.
而索引系统(这里主要围绕着B+ tree展开).其作用在于,能够根据某个字段或者多个字段,加速其查找.也可以说,索引是在原始存储的数据中,所抽象出来的一层将数据中的键值根据某种方式组织成的便于查找的数据结构,比如说在本次lab中,就会将文件中的数据中的某个键组织成一颗B+树,之后关于对文件的增删查操作都会现在B+ 树上进行,找到目标后,就返回其对应的Page.这样显然避免了对整个文件的遍历.
此外,一个原始数据文件可以有多个索引文件,每个不同的索引文件可以代表不同键值处所构造的索引.在本次lab中,通常是将一个文件有一个索引文件实现的.此外,索引还有稀疏或者稠密之分,稠密的索引就是一个文件中所有Record都有索引项的方式,否则就是稀疏的.
2) B+树
首先B+树有几个基本的特点:
- 除了leaf节点之外,不存储实际的数据.
- 叶子结点以链表的方式连接起来,所以B+树具有范围查找的能力,相比之下,B树的leaf节点并没有串起来,所以没有范围查找的能力.
- 每个leaf的高度是一样的,相比一般的二叉树,其增长过程是从leaf开始,自下向上的,很多树都是自顶向下插入的.
此外,由于这里数据库系统做I/O操作的基本单位是Page,而一个B+树节点也就是一个Page.因此,在这里,如果将一个文件(只有一个索引键)对应一个B+树的话,文件中的所有数据都在leaf上,想要定位一个数据就得查找到其所在的leaf Page.
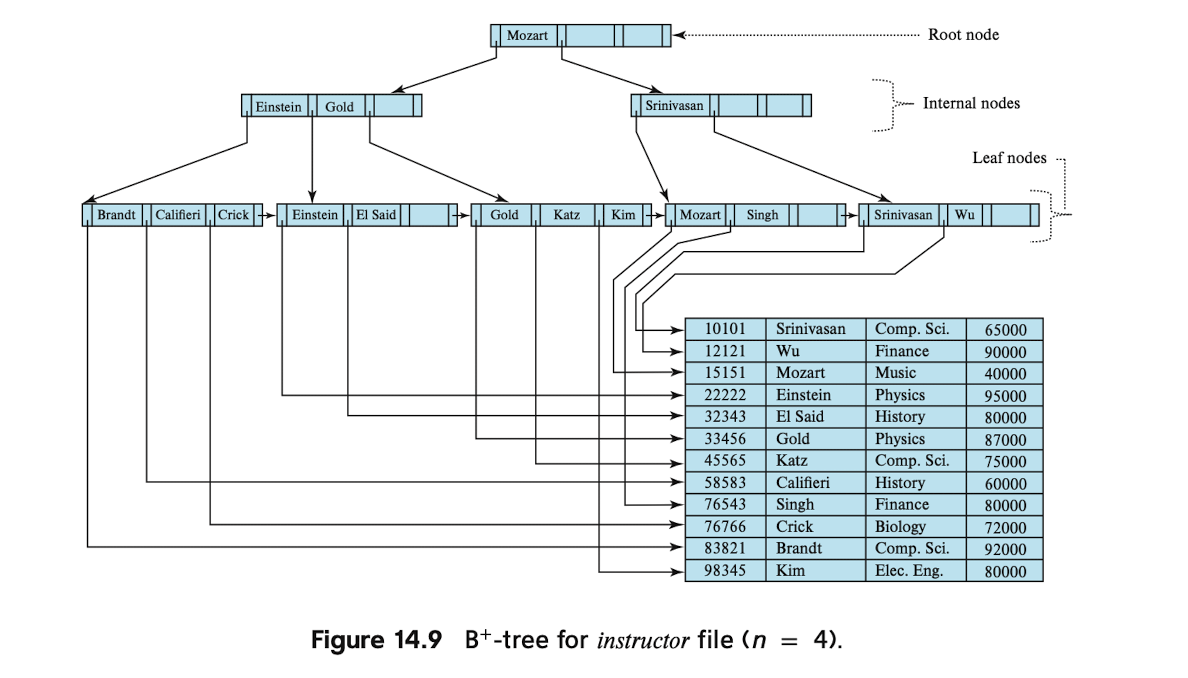
关于检索,插入,删除等操作的执行过程,在下面的每个练习中会细说.
1.B树系列为什么适合磁盘上的读写操作?
B树相比于红黑树等数据结构,不在限制于“二叉”的性质,而且一个节点可以包含多个数据项,所以一般情况下,相同的数量的数据n,一个B树所呈现的高度更低,对于存储于磁盘上的数据,操作系统I/O的基本单位是一个block,此外在读取或者写数据时,I/O时间要显著多于CPU时间,因此节省I/O时间是提升读写磁盘数据的关键.
由于B树作为多叉树的特点,可以有更低的高度,和更少的节点,一般B树一个节点对应disk上的一个block,因此访问block的次数大大减少,进而导致I/O开销大大减少,一个节点可以有多个数据项也充分地利用了disk分块作为单位读写的特点.
虽然一个节点有多个数据项的特点导致在查找时,需要多花费时间在遍历一个节点上,但是由于局部性的特点,这点开销不大.
2.B树,B+树的区别有什么?
在实际的磁盘存储中,B+树用得比B树多一些.
(1).B+树只有叶子结点保存数据,再结合B+树平衡的特性,任何查找工作经过的路径长度都是相同的,因此B+树的查找开销是更加稳定的.
(2).B+树的叶子结点之间是具有指针连接的,这点使得B+树具有范围查找的能力.
(3).B+树的中间节点不保存数据,
2.实现过程
1) Exercise 1: BTreeFile.findLeafPage()
这一部分的实现是比较简单的,类似于一般的二叉树的递归,但是B+树是多叉树,因此每一步向下递归的过程中,还会涉及到对于一个节点上的数据项的遍历.
private BTreeLeafPage findLeafPage(TransactionId tid, Map<PageId, Page> dirtypages, BTreePageId pid, Permissions perm,
Field f)
throws DbException, TransactionAbortedException {
// some code goes here
BTreePageId pageId = pid;
while (pageId.pgcateg() != BTreePageId.LEAF) {
Page page = getPage(tid,dirtypages,pageId,Permissions.READ_ONLY);
int pgcatag = pageId.pgcateg();
if (pgcatag == BTreePageId.INTERNAL) {
Iterator<BTreeEntry> it = ((BTreeInternalPage) page).iterator();
BTreeEntry entry = null;
boolean isfound = false;
while (it.hasNext()) {
entry = it.next();
Field field = entry.getKey();
if (f == null || field.compare(Op.GREATER_THAN_OR_EQ, f)) {
pageId = entry.getLeftChild();
isfound = true;
break;
}
}
if (!isfound && entry != null) {
pageId = entry.getRightChild();
}
}
}
return (BTreeLeafPage) getPage(tid,dirtypages,pageId,perm);
}直到遍历到一个leaf
Page即为到达终点,其中需要注意的是对于null来说,一直向左递归就可以了,还有关于向下递归的条件,究竟应该是”大于等于“还是“大于”.我之前是按照大于做的,但是这样会导致错误,尤其是对于有重复的情况.在此举一个例子:

对于图中的情况,如果等到“>"才向下左递归的话,如果想要查找1,这样递归到根下面的一层后,就会朝最右方递归,这明显导致所读的leaf Page数据不全的情况,如果想要查找的是2的话,则会递归到[2,3,3,3]这一个叶子结点,仍然是不能得到一个含有2的完整的leaf Page.对于所要查找的值,正好等于一个中间节点(下一层就是leaf的情况),如果递归到左子则不一定含有该数值,但是由于leaf Page相连的特点,还是可以遍历到下一个leaf Page,进而达到完整地遍历该数值对应的leaf Page的.如果是“>”的条件就向左下遍历,那么容易造成缺页,进而无法完整遍历该数值所在的leaf page.
B+树的叶子结点中的key呈现单调不下降的特点,当叶子进行分裂并将m/2项放到上一层节点的时候,未必就能保证该Tuple右边的一定就大,左边的就一定要小,它们还有可能是相等的.所以在这里我认为,不能认为左子树一定是小于的,右子树一定是大于的,左右子树都可以有等于的情况在其中.
2) Exercise 2: Splitting Pages
public BTreeInternalPage splitInternalPage(TransactionId tid, Map<PageId, Page> dirtypages,
BTreeInternalPage page, Field field)
throws DbException, IOException, TransactionAbortedException {
BTreeInternalPage newPage = (BTreeInternalPage) getEmptyPage(tid,dirtypages,BTreePageId.INTERNAL);
int maxEntry = page.getMaxEntries(),index = 0;
BTreeEntry midEntry = null;
Iterator<BTreeEntry> rit = page.reverseIterator();
int maxSize = page.getMaxEntries();
for (int i = 0; i < maxSize / 2 ; i ++) {
BTreeEntry entry = rit.next();
page.deleteKeyAndRightChild(entry);
newPage.insertEntry(entry);
}
midEntry = rit.next();
page.deleteKeyAndRightChild(midEntry);
updateParentPointers(tid,dirtypages,page);
updateParentPointers(tid,dirtypages,newPage);
BTreePage parentPage = getParentWithEmptySlots(tid,dirtypages,page.getParentId(),field);
((BTreeInternalPage) parentPage).insertEntry(new BTreeEntry(midEntry.getKey(),page.getId(),newPage.getId()));
updateParentPointers(tid,dirtypages,(BTreeInternalPage) parentPage);
dirtypages.put(parentPage.getId(),parentPage);
dirtypages.put(page.getId(),page);
dirtypages.put(newPage.getId(),newPage);
if (field.compare(Op.GREATER_THAN_OR_EQ,midEntry.getKey())) {
return newPage;
}
return page;
}这一部分的实现相对来说比较简单,这里只列举splitInternalPage.
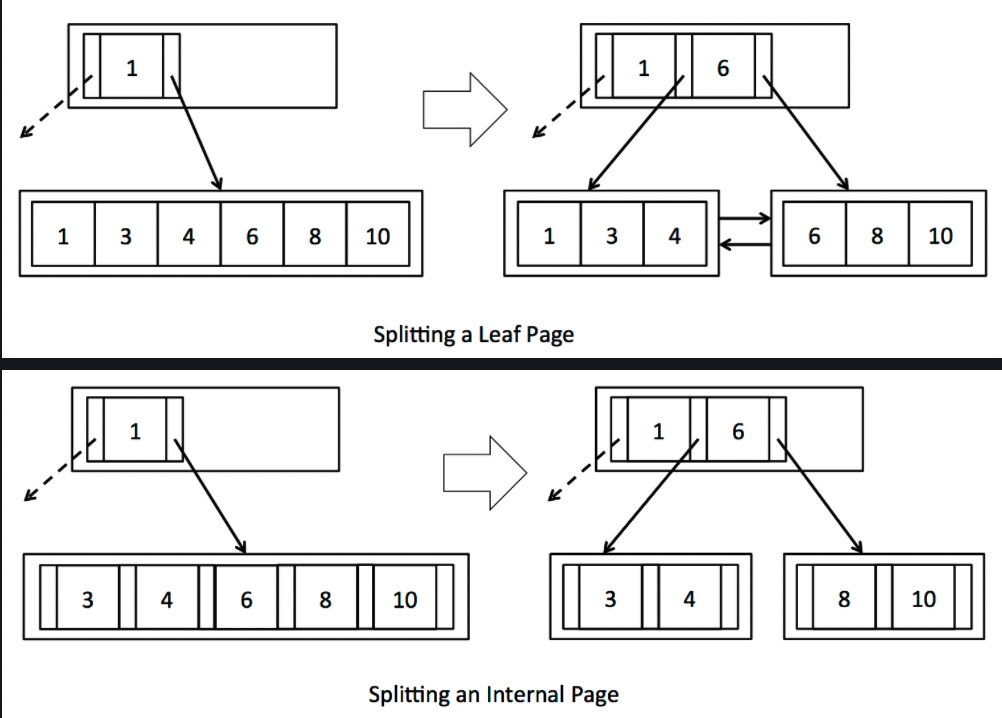
其中分裂的规则就是两方对半平分,至于Internal,Leaf的主要区别就在于,是否需要将第m/2个节点移除,由于B+树的特点就是所有的叶子结点必须涵盖所有的数据,因此当leaf
Page进行split时无需将第m/2个节点移除,如果是Internal的话,则需要进行移除.
所以在splitInternalPage的实现中,主要分为如下过程:
- 将page的部分节点移除(对半平分),并且插入到newpage中.
- 对于最后一个移除的要进行一定的特殊处理,这一个不需要插入到newpage中.
- 更新newpage和page的孩子节点.
- 使用
getParentWithEmptySlots(递归地)获取这两个节点的父节点. - 将mid项插入(注意左右child的设置),到父节点.
- 缓存脏页并返回.
理解了split操作后,就可以将insert概括为,首先findLeafPage找到目标应该所在的leaf
Page,然后根据其当前大小判断是否要进行split,如果不需要就直接加入,否则就将其分裂出一个new
leaf
Page,并且加入一个新的中间结点,如果中间节点也出现了超出数量的情况,则继续递归到中间节点,并执行split,再加入新的中间结点,以此类推,知道不需要分裂或者到达根节点为止.
3) Exercise 3: Redistributing pages
public void stealFromLeftInternalPage(TransactionId tid, Map<PageId, Page> dirtypages,
BTreeInternalPage page, BTreeInternalPage leftSibling, BTreeInternalPage parent,
BTreeEntry parentEntry) throws DbException, TransactionAbortedException {
Iterator<BTreeEntry> rit = leftSibling.reverseIterator();
int totalNum = page.getNumEntries() + leftSibling.getNumEntries();
BTreeEntry bTreeEntry = null,newBtreeEntry = null;
BTreeEntry oldParentEntry = new BTreeEntry(parentEntry.getKey(),
leftSibling.reverseIterator().next().getRightChild(),
page.iterator().next().getLeftChild());
page.insertEntry(oldParentEntry);
while (page.getNumEntries() < totalNum / 2) {
bTreeEntry = rit.next();
leftSibling.deleteKeyAndRightChild(bTreeEntry);
page.insertEntry(bTreeEntry);
}
newBtreeEntry = rit.next();
leftSibling.deleteKeyAndRightChild(newBtreeEntry);
updateParentPointers(tid,dirtypages,leftSibling);
updateParentPointers(tid,dirtypages,page);
parentEntry.setKey(newBtreeEntry.getKey());
parent.updateEntry(parentEntry);
updateParentPointers(tid,dirtypages,parent);
dirtypages.put(page.getId(),page);
dirtypages.put(leftSibling.getId(),leftSibling);
dirtypages.put(parent.getId(),parent);
}关于删除操作需要涉及到的操作有steal和Merge,前者的原则仍然是对半平分.
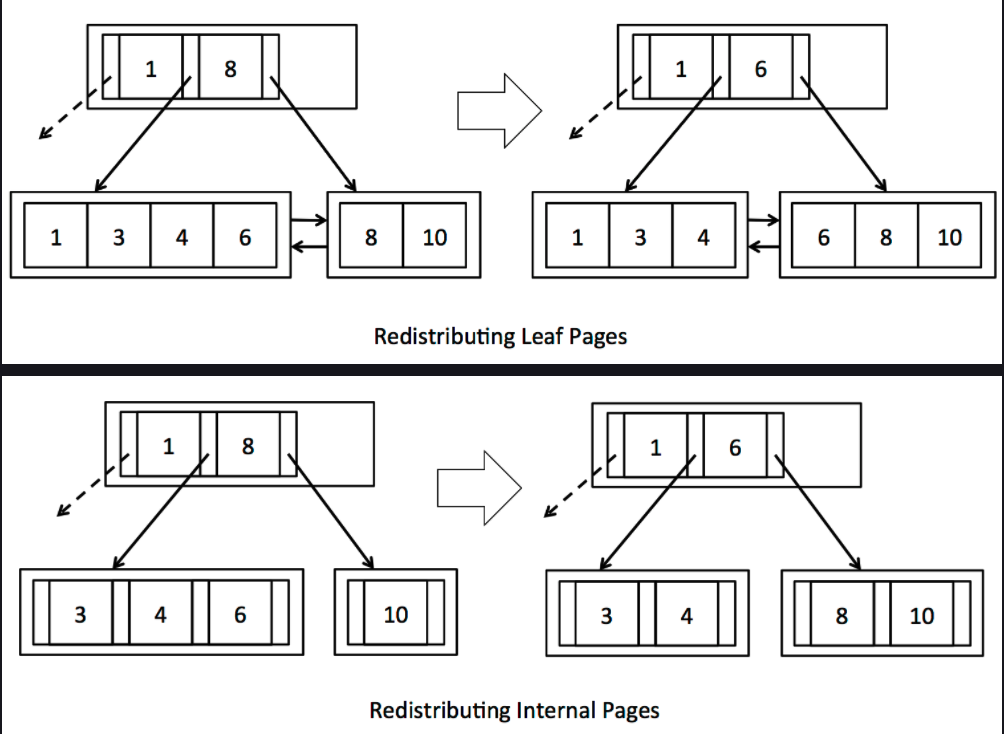
4) Exercise 4: Merging pages
public void mergeInternalPages(TransactionId tid, Map<PageId, Page> dirtypages,
BTreeInternalPage leftPage, BTreeInternalPage rightPage, BTreeInternalPage parent, BTreeEntry parentEntry)
throws DbException, IOException, TransactionAbortedException {
Iterator<BTreeEntry> entryIt = rightPage.iterator();
BTreeEntry oldparentEntry = new BTreeEntry(parentEntry.getKey(),leftPage.reverseIterator().next().getRightChild(),
rightPage.iterator().next().getLeftChild());
leftPage.insertEntry(oldparentEntry);
while (entryIt.hasNext()) {
BTreeEntry entry = entryIt.next();
rightPage.deleteKeyAndLeftChild(entry);
leftPage.insertEntry(entry);
}
updateParentPointers(tid,dirtypages,leftPage);
setEmptyPage(tid,dirtypages,rightPage.getId().getPageNumber());
deleteParentEntry(tid,dirtypages,leftPage,parent,parentEntry);
updateParentPointers(tid,dirtypages,parent);
dirtypages.put(leftPage.getId(),leftPage);
dirtypages.put(rightPage.getId(),rightPage);
dirtypages.put(parent.getId(),parent);
}其中以mergeInternalPages为例,这里的实现过程(将右leaf
Page合并到左leaf Page)如下:
- 将需要移除的BTreeEntry追加到left page中(注意child的设置).
- 将所有right page中的项移除,并insert到left leaf page.
- 更新left page的child的父母节点,将已经合并的righht page设置为null,移除父节点中对应的项.
- 缓存脏页.
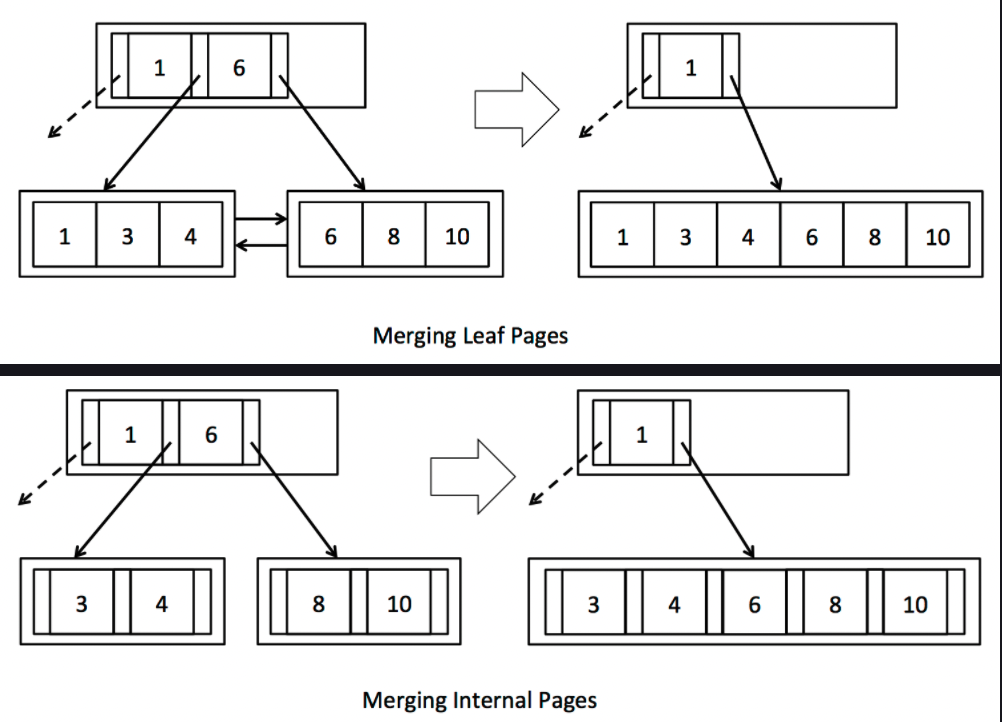
在这里关于merge的实现,其中中间节点和leaf结点的区别在于,同样都需要将对应的某个parent进行移除,但是移除的时候是否还需要将这个移除的项加入到子节点中呢?如果是leaf
page,直接移除就可以,其他不需要做什么,如果是中间节点,则还需要将移除的节点项加入到某个child
Page中.因为在其他的操作中,都不会破坏leaf page维护全部数据的性质.
接下来可以简单地梳理一下delete过程,仍然是先找到目标所在的leaf
page.然后检查该leaf
page的数量,如果去掉一个后不少于一半就直接移除该项,否则进行steal或者merge,首先进行steal,如果steal之后发现仍然有一方数量不足就进行merge.一直向上递归,知道递归到某个节点的数量符合要求或者到达根节点.
3.小结
这个lab怎么说呢,B+树的实现方面细节比较多,这算是一个难点,但是这次lab并不会涉及到太多关于整个database的架构的理解.至于这次lab的实现,我有个很遗憾的地方在于,并没有通过附加题中的BTreetest.我想应该是我在Lock Manager方面出的问题吧,暂时先鸽了.