编译器后端以及优化相关的基础理论

0. LLVM基础

1) 系统总览

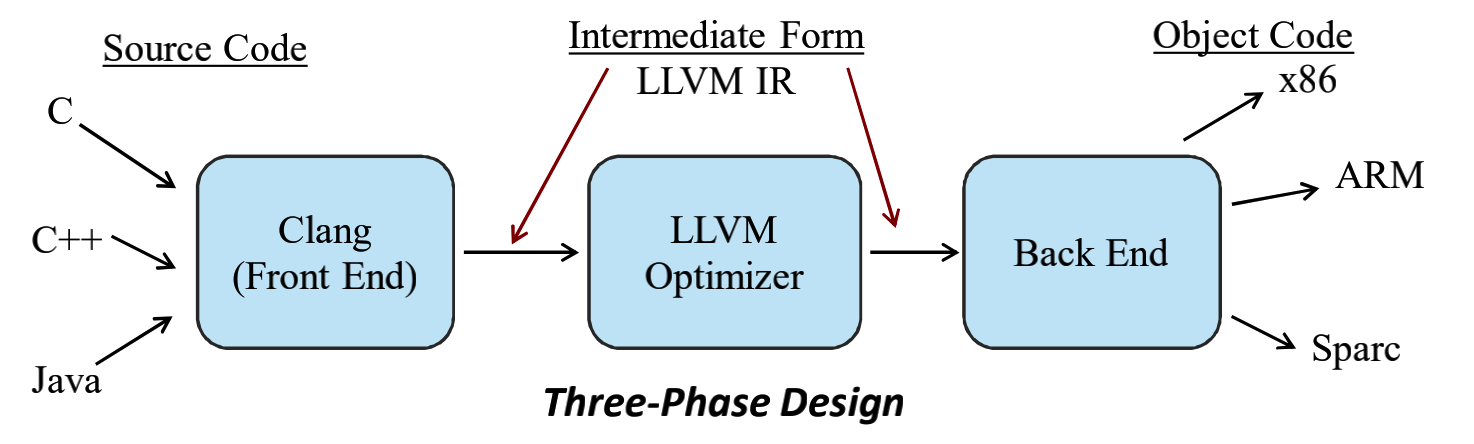
其中关于LLVM优化器是又一个个Pass所组成的, 每一个Pass根据IR分析收集一些信息, 进而调整IR达到优化的效果.LLVM有一套虚拟指令集, 看上去类似于汇编语言的伪代码, LLVM IR的形式与此有关.

其中Clang的结果是一个AST树, 比如说对于代码:

int main() {
	int a = 5;
  int b = 3;
  return a - b;
}

可以得到如下形式的AST树:

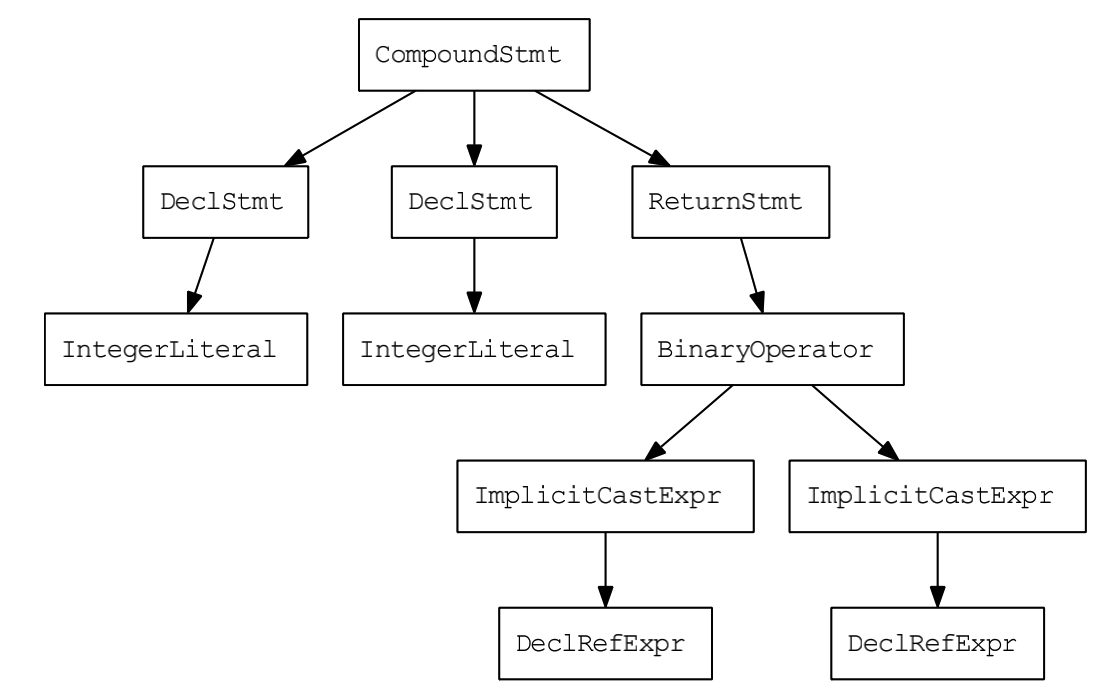
完整的LLVM编译阶段:Source code —> Clang AST —> LLVM IR—> SelectionDAG—>MachineInst—>MCInst/Assembly

2) LLVM Program Structure

主要涉及到以下四个主要概念:

  • Module. 包含了一些Functions和GlobalVariables,可以视为对一整个程序的抽象.
  • Function. 包含了一些基本块以及参数.这个概念和C语言中的概念是非常像的.
  • BasicBlock, 只一连续的指令所组成的代码段, 不涉及到分支、跳转、条件,只要一个Block被执行, 其中所有指令都会执行到.
  • Instruction, 相当于一个个指令.

下面的这个图总结的很直观:

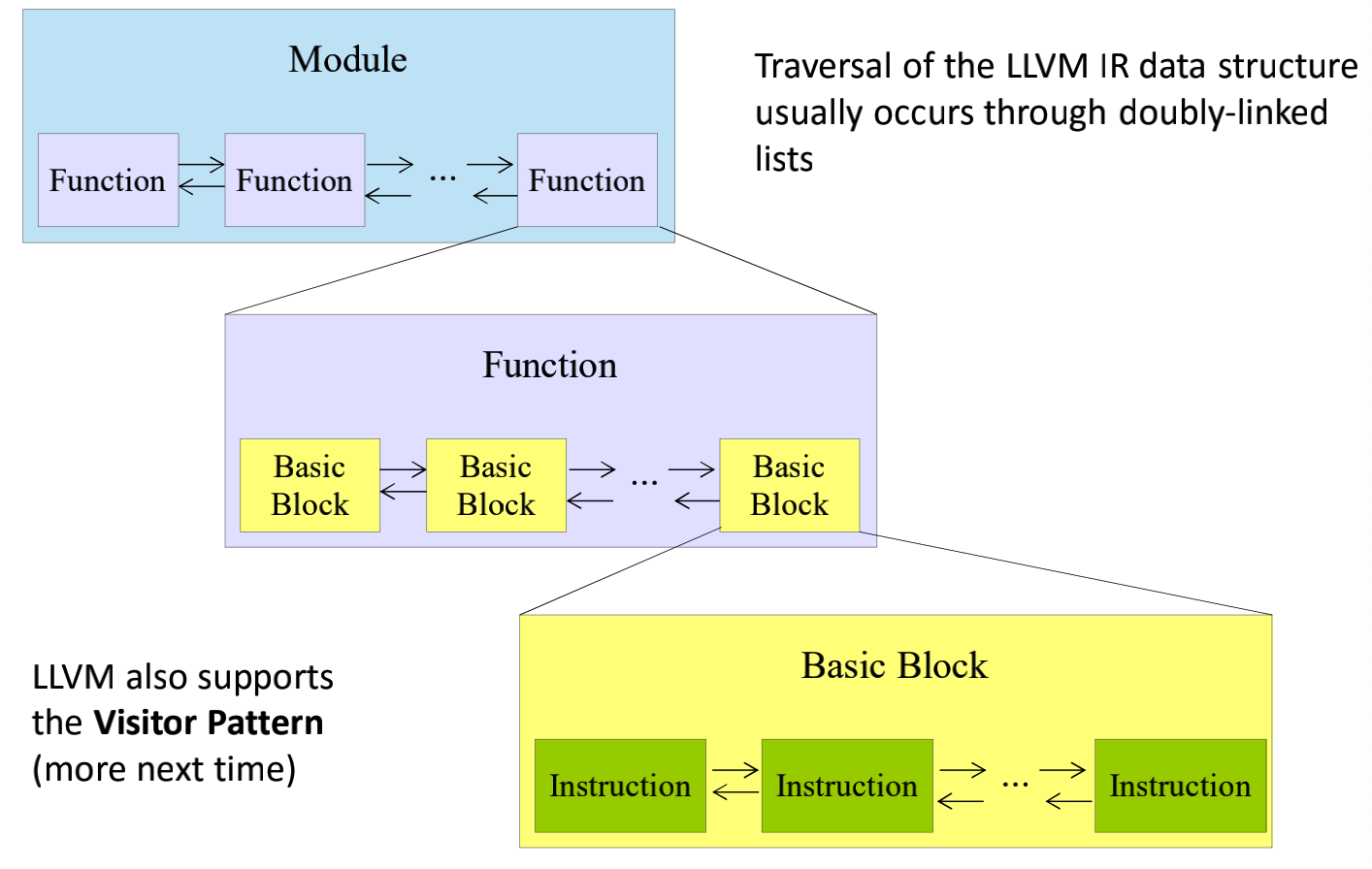
image-20221230230244724

3) More on the LLVM Compiler

Data Structures

首先需要提到的是string, 为什么不推荐常规C/C++程序一样直接使用char*或者std::string, 作为字符串呢? 因为前者使用了'\0'表示字符串末尾, 这种方式对于字节字符串来说是不太合适的.至于后者在性能上不是太优秀.其使用方式大致如下:

StringRef("myfunc", 6)
std::string("myfunc") //相当于

如果使用.str()可以获取其对应的std::string.此外关于输入输出“std::cout”应该使用的是outs(),errs(),null()等.如下所示:

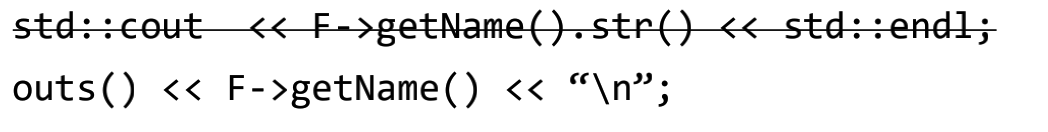
image-20221230232617555

不仅仅如此, 相比C++中的STL, 比较建议使用的是LLVM提供的一些数据结构, 其中包含这些:

ImmutableSet, IntervalMap, IndexedMap, MapVector, PriorityQueue, 
SetVector, ScopedHashTable, SmallBitVector, SmallPtrSet, SmallSet, 
SmallString, SmallVector, SparseBitVector, SparseSet, StringMap, StringRef,StringSet, Triple, TinyPtrVector, PackedVector, FoldingSet, UniqueVector,ValueMap

Class Hierarchy

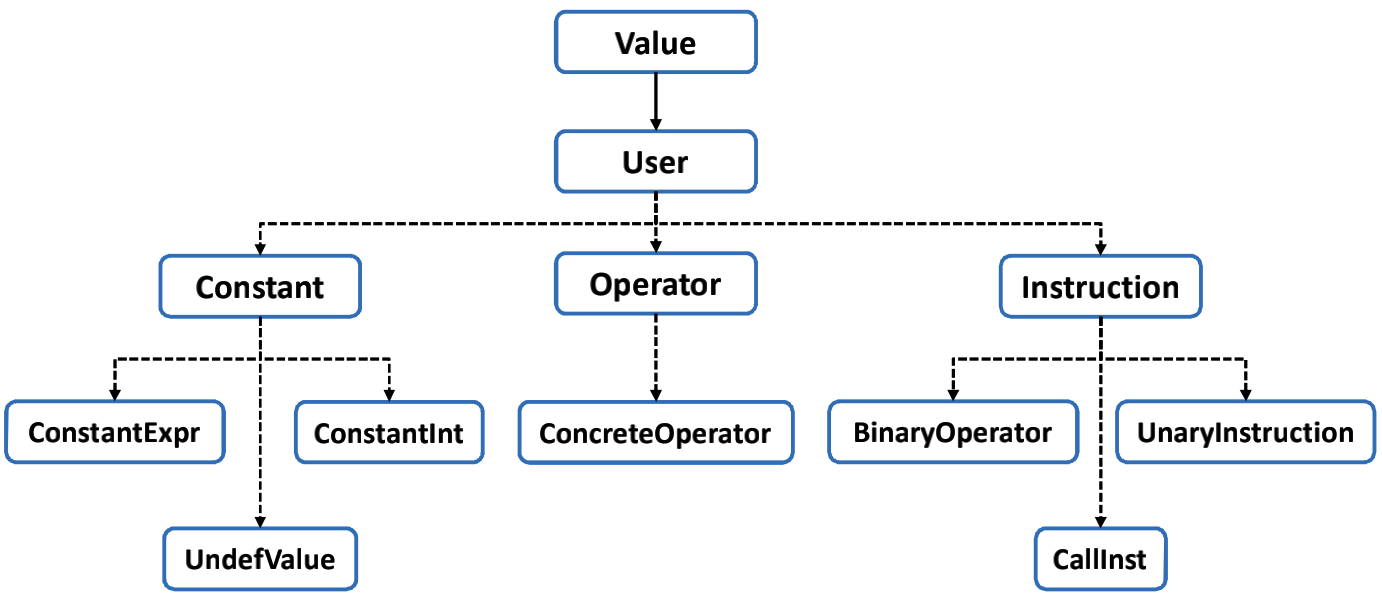
image-20221230232824248

Casting and Type Introspection

除此之外, 还有isa<Argument>(v), cast<Argument>(v), dyn_cast<Argument>(v)等比较重要.这三者分别相当于判断v是否是一个Argument class对象、static_cast、dynamic_cast等等.

Iterators

其中包含Module::iterator, Function::iterator, BasicBlock::iterator, Value::use_iterator, User::op_iterator.相关的使用实例代码如下:

for (Function::iterator FI = func->begin(); FI != func->end(); ++FI) {
		for (BasicBlock::iterator BBI = FI->begin(); BBI != FI->end(); ++BBI) {
			outs() << “Instruction: ” << *BBI << “\n”;
		} 
}
for (inst_iterator I = inst_begin(F), E = inst_end(F); I != E; ++I) { 
		outs() << *I << “\n”;
}

此外还有其他使用建议:

  • 主要遍历对象时的修改, 这些iterator都是no const的.
  • 最好用++i而不是i++.

Visitor Pattern

这里还介绍了一种常用的访问者模式的设计模式. 对于给定的对象(比如说Module, Function等)我们通过专门设计的一个class来对这些进行访问, 也可以进行修改. 这种类会实现一些函数来访问特定的对象, 这些函数往往使用引用类型的参数.实例代码如下:

image-20221230234038887

LLVM中也提供了一些API用来对IR进行增加删除等修改操作.

1. 局部优化

局部优化指的是局限于单个basic block之中的优化方法.这其中涉及到的最最基础的概念就是Basic block和Flow graph, 前者是三地址语句的序列, 后者是以基本块作为节点的图.其中前者的更准确的定义是:不涉及到跳转、分支、条件, 只会顺序执行的最长代码段. 后者通过图的方式描述了各block之间的流动状况.

主要介绍两种方法, 第一种是value numbering.通过查找basic block中的冗余表达式, 如果冗余的表达式有相同的计算结果, 那么就将其重用即可. 第二种方式是基于DAG的方法.

1) Value Numbering

如何判断一个程序块中的表达式冗余呢? 首先起码在形式上完全相同.比如说下列中的:

# 重写前
a <- b + c
b <- a - d
c <- b + c
d <- a - d

就比如说上面就有两对符合这种特征的, 但是其中只有a - d才可以说是符合冗余的.因为还有一个重要的特征, 即相同的表达式之间, 其中没有发生参数又被赋值的情况, 比如说b+c中, 其中在第二行出现了对b的赋值, 因此b + c就不算是冗余表达式.所以总的来说, 冗余的表达式特点如下:

  • 形式相同.
  • 每两者之间没有发生参数被赋值的操作.

因此可以重写为:

# 重写后
a <- b + c
b <- a - d
c <- b + c
d <- b

但其实冗余还有更加复杂的情况, 比如说“形式不同”的情况, 就如同下面的代码中:

a <- b * c
d <- b
e <- d * c

其中形式不同, 但其实也符合冗余的特点, 也应该进行优化.因此其实冗余表达式的查找和判断不是一件容易的事, 因此需要考虑设计新的方法.在这里主要介绍的是Local Value Numbering,下面简称LVM.下面简要说明该方法.

该方法需要用一个map表示将name, const, expression映射到值编号.最初是空的.在LVM中, 其输入是一个三地址表达式序列, 可以代表一个基本块.在进行计算时, 顺序地遍历该序列,对于每个表达式, 首先查找L和R是否处于map中, 如果有就使用其编号就可以, 没有的话就对其分配一个(从0开始自增).之后再给予“value(L) op value(R)”来产生一个散列key, 并在map中查找, 如果有,表示该表达式冗余, 直接使用之前的所求的value就可以.否则对这个key分配一个新的编号,还需要对其对应参数的value进行替换.其中伪代码描述如下:

其中有具体例子如下:

a <- b + c # value(b) = 0, value(c) = 1, value(0+1) = 2, value(a) = 2
b <- a - d # value(a) = 2, value(d) = 3, value(2-3) = 4, value(b) = 4
c <- b + c # value(b) = 4, value(c) = 1, value(4+1) = 5, value(c) = 5
d <- a - d # value(a) = 2, value(d) = 3, value(2-3) = 4, value(d) = 4

其中发现value(2-3)前后一样, 因此判断为冗余的表达式.判断出后,便进行重写.

拓展LVM算法

  • 交换运算对于一些可交换的运算来说, 比如说a + b和b + a,两个表达式的应该被视为相同的key, 如果说这两个表达式所产生的key分别是0+1和1+0, 对于可交换运算来说, 应该采用某种方式统一次序, 进而可以以统一的方式代入map.
  • 常量合并.

关于对冗余代码进行重写时, 还有一个问题, 比如说下面的这种情况:

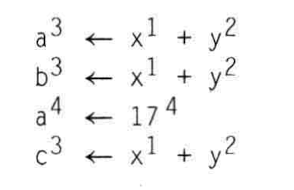
image-20221229110219635

可以确定第1, 2, 4行的式子是冗余的, 但是当需要重写时, 第四行的式子不能重写为c <- a.因为a已经被修改.应对这种问题, 可以增加一个从编号到name到map.当某个name的编号经过赋值而发生改变时, 就将其所属编号list移动到另一个编号list.当需要进行重写时, 就通过该map查找对应的编号下的list就可以了.

另一种方法如下, 每次对某个值进行重新设置编号时, 就分配一个新的name.比如说:

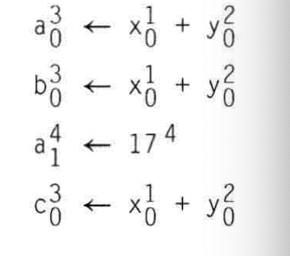
image-20221229111135143

2) 基于DAG的优化

这里主要参考龙书学习.这种方法的基本思路, 在于将一个基本块的转化为一个DAG.其实这种方法和上面提到的局部值编号方法本质上是相同的, 只不过形式上略有差别.其实上面的方法中主要针对的是局部公共子表达式的问题.

寻找局部公共子表达式

这里的局部公共子表达式也就是上面所说的冗余的表达式, 只不过是不同教材中的不同表达方式罢了.

其中情况如上.书中还提到了一种情况就是非冗余表达式, 但其值可以确定完全一样的情况, 这种情况需要借助DAG中的代数恒等式来确定.

对于一个块的输出节点, 也就是需要被后续的块所引用的变量, 我们称之为出口处活跃. 这需要借助数据流分析来完成.

消除死代码

基于DAG删除死代码的操作可以以如下的方式实现, 从DAG上删除所有没有附加活跃变量的跟节点.重复,直到没有可以删除的为止.也就是说, 在生成的DAG中, 如果一个节点是跟节点, 并且其对应的变量并没有作为后续block的输入变量(也就是不是活跃变量), 就应该将该结点移除.

代数恒等式

2. 数据流分析基础

数据流分析会遍历流图, 收集运行时可能发生的有关信息.之后往往需要根据分析结果采用某种方法调整IR, 从而达到优化的目的.流图是一种以基本块为节点的图, 其中在数据流分析中, 所采用的单位(也就是书中所说的程序点)指的是相邻指令语句之间的间隔, 我们根据需要采集的信息抽象出整个程序的状态, 关于这些状态的值在程序点流动时的变化过程是数据流分析中最关注的.

在各种程序点中的, 一个基本块内部相邻的程序点之间没有发生信息的变化, 也就是语句n执行完和语句n+1执行前是一致的, 如果是跨越了基本块的相邻程序点也是这样的.所谓执行路径就是流图中程序点的连续序列.

如果要举例子的话, 如下所示:

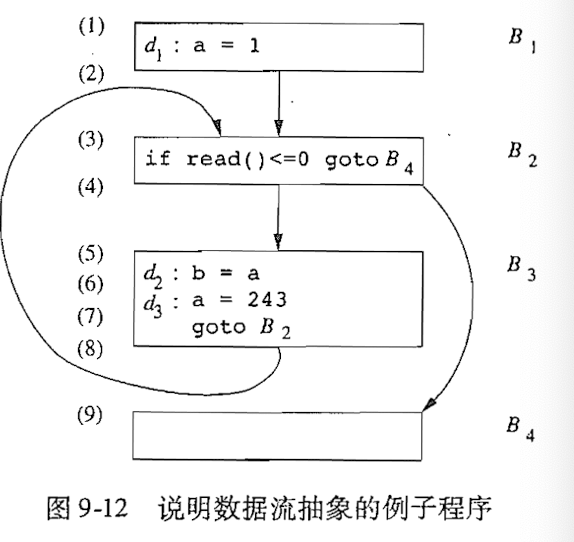
image-20221230173044558

由此图可知, 一个程序的路径可以不只一条.

既然上面就提到了, 数据流分析是需要收集信息并且分析信息在流动时的变化情况的, 关于这些“信息”.在这里为了更准确地描述, 对每个语句s的前后的数据流志极为IN[s]和OUT[s].并且定义传递函数, 即OUT[s] = fs(IN[s]).关于控制流约束就如同上面所说的:

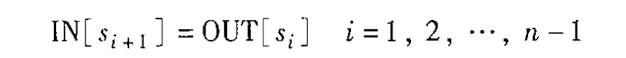
​ image-20221230174048309

此外对于基本块也有这种定义IN[B]和OUT[B].

1) 到达-定值分析

在经过一个程序点时, 一个变量有可能被赋值(改变值,即为定值).

定值分析问题就是分析在给定的d和p点之间对于某个变量x是否发生定值, 如果发生定值就称该变量被kill.

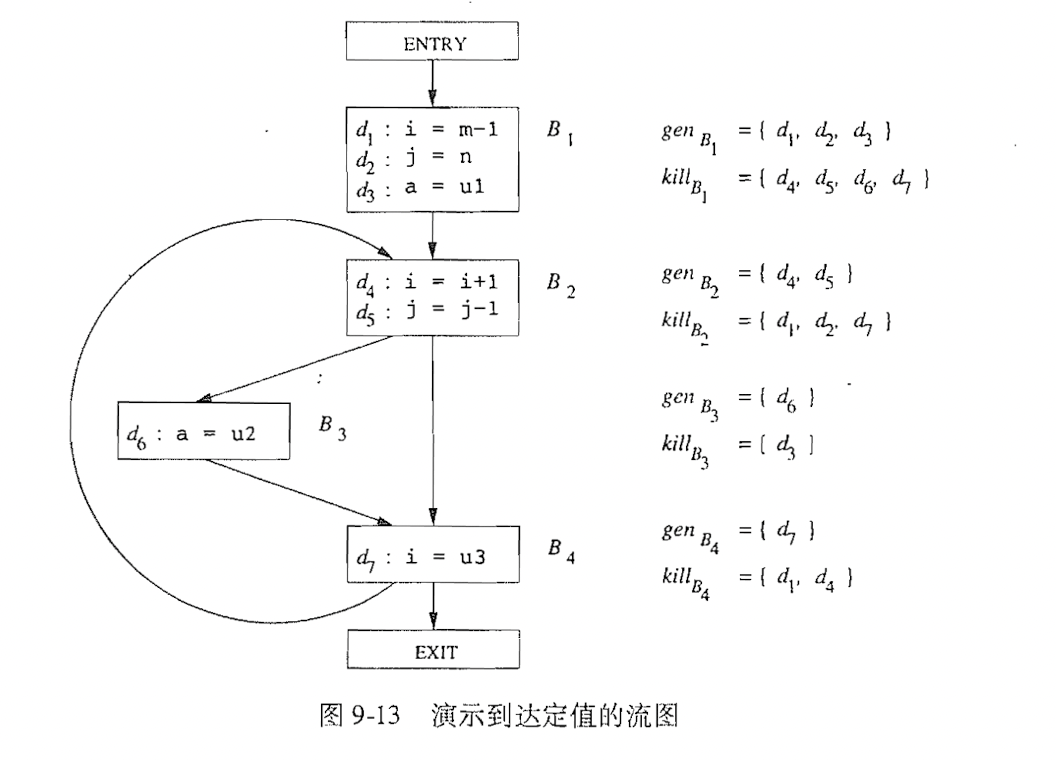
image-20221230175222999

其中gen表示的是某个块中的定值, kill表示的是后续会将block中的定值kill的定值.关于传递方程,这里是一种“生成-杀死”形式的传递函数, 如下这种形式:

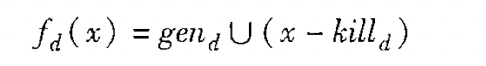
image-20221230203251499

之后可以推导出相关的算法.该算法已经给定了流图中每个基本块B的kill集和gen集,要求我们求出每个基本块的入口点和出口点的定值的集合, 也就是IN[B]和OUT[B].

该算法有伪代码描述如下:

image-20221230203811120

2) 活跃分析

活跃分析用于想要知道某个变量x和程序点p, x在点p上是否会在流图中的某条从p出发的点中使用.如果是则称为活跃的, 其中有关的应用是寄存器分配, 因为当一个变量被存放到寄存器中后, 我们需要通过这个变量在后面是否活跃从而确定是否可以使用该寄存器.

这里仍然是采用IN、OUT的方式, 不过在这里定义的是一个表示变量是否活跃的BitSet.具体的相关集合指的是use和def.前者指的是某一个变量被使用, 后者指的是某一个变量被定值.

输入指的是一个已经计算出use和def的流图,因此相关算法如下:

image-20221230204825499

要求输出是一个IN[B]和OUT[B].

3) 可用表达式分析

这里提到的可用表达式也就是前面所提到的冗余表达式, 也就是对于相同形式的表达式, 其结果有没有发生改变, 如果仍然没变, 就可以复用之前的结果.至于判断是否可用的方式, 则是从入口点到p, 如果在此期间x或者y发生了定值, 因此可以说杀死了这个表达式.

相比到达-定值问题中所提到的杀死或者生成, 这里所针对的对象不再是变量而是表达式.其用途在于寻找全局公共子表达式. 在解决该问题的算法中, 涉及到的抽象有gen和kill, 前者表示生成的表达式的集合, 后者表示被B所杀死的表达式的集合.相关的算法的伪代码描述如下:

对于以上三种问题, 采用了类似的模式去抽象、定义.彼此之间的不同点如下:

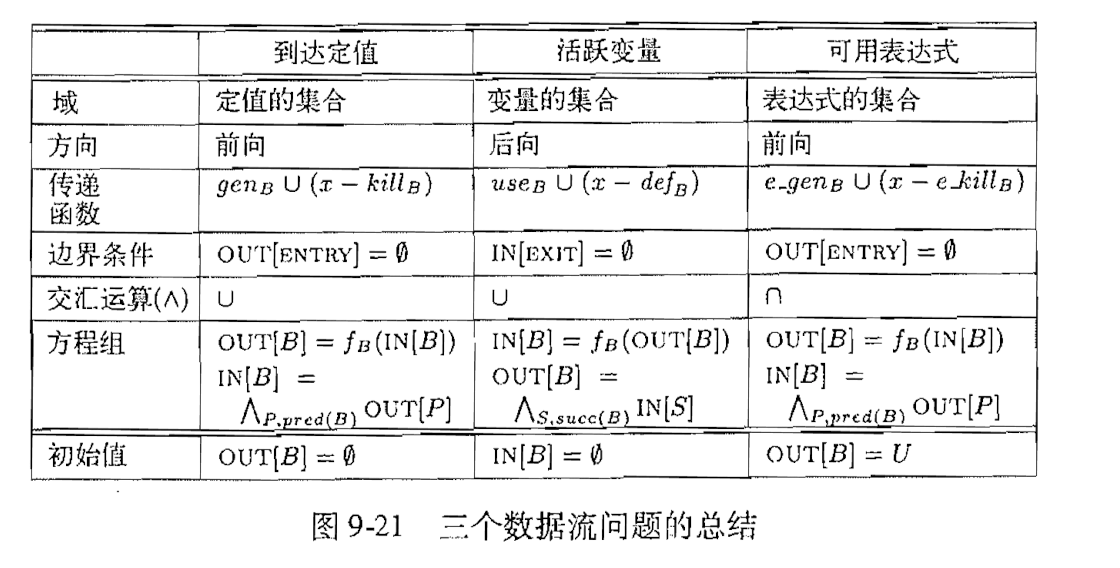
image-20221230205118710

3. 静态单赋值形式

静态单赋值是一种中间表示形式, 保证每个变量只会被赋值一次, 在使用某个变量前一定被定义了. 在原始的IR中, 一个变量可以分割成多个不同的版本, 每个定义对应了一个版本, 每个版本附带上不同的下标保证新的变量名没有任何重名的.,举个简单的例子:

# 非SSA代码
y := 1
y := 2
x := y
# SSA代码
y1 := 1
y2 := 2
x1 := y2

其实从非SSA中可以看出, y的赋值操作是完全没有必要的. 因此可以体现出一些优化的潜能.SSA所涉及到的优化算法有:常数传播、值域传播、稀疏有条件的常数传播、消除无用代码等等.

对于静态单赋值形式有一个主要问题,在于对于分支, 如下代码:

if (flag) x1 = -1; else x2 = 1;
x3 = Phi(x1, x2);

其结果要么是来源于x1, 要么是来源于x2, 该函数表示将两者合并起来的结果.如下所示:

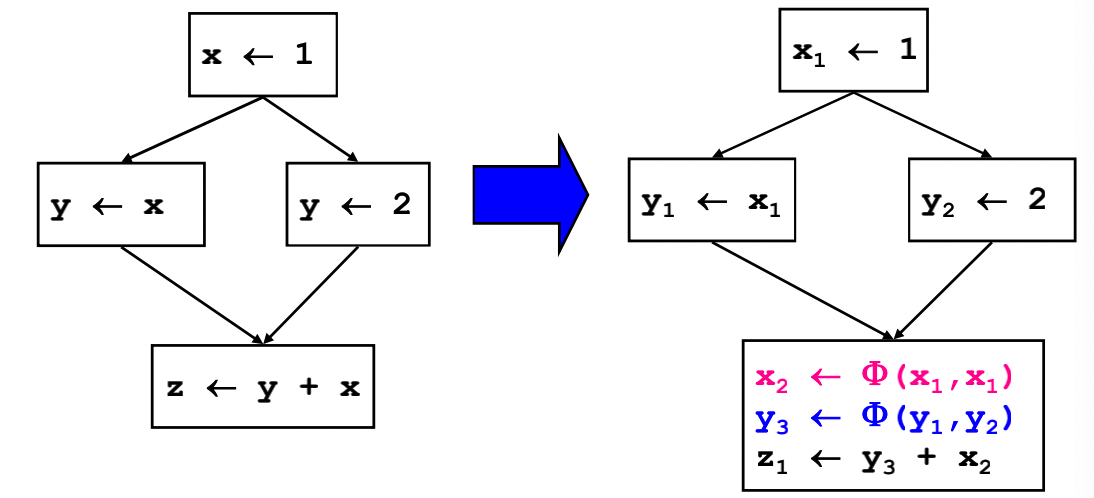
image-20221231111740233

其实还可以进一步化简, 将其中的x2那一行删除.还有一个例子如下:

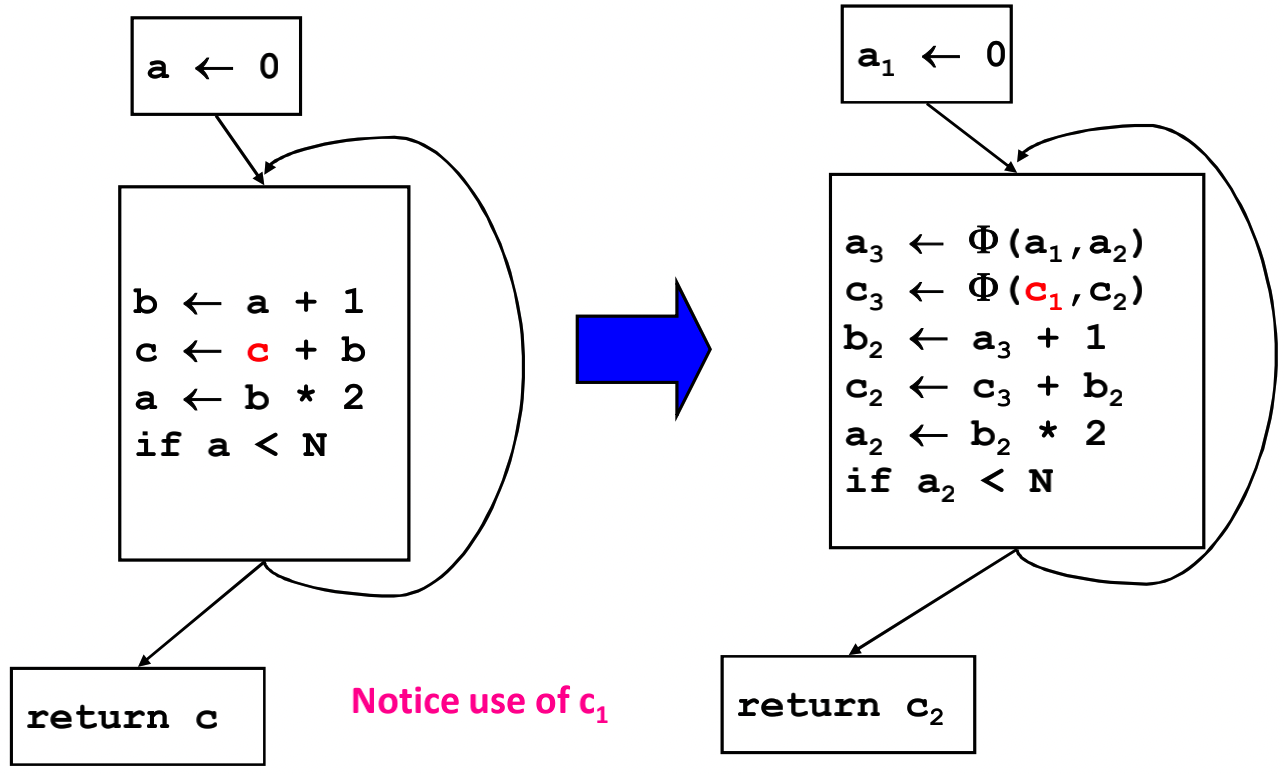
image-20221231112440999

这一部分的算法简而言之可以分为三步:

  • 找出内含变量定制的基础块, 及其支配边界.
  • 插入Phi结点.需要插入在控制流图的汇聚点处, 只要在汇聚点之前的分支中出现了对某个变量的修改, 就需要在该汇聚点插入针对该变量的Phi结点, Phi结点的操作数是分支路径中重新定义的变量.
  • 变量重命名.

接下来详细地说明插入Phi结点和变量重命名的算法.

image-20221231113824658

4. 循环优化

关于循环在数据流图中的准确定义: 是一系列(S)数据流图中的节点, 其中包含一个header节点, 遵循如下几种性质:

  • 某个(些)节点中有节点指向header节点.
  • header也有一个指向其他节点的路径.
  • 外部的其他节点只能通过heder进入S.

1) 必经结点

我们的首要任务是找到循环, 其中必经结点的概念非常有用.这个概念很好理解, 就和它的字面意思一样.必经结点在某些教材中也被称为支配结点.

寻找必经结点的算法

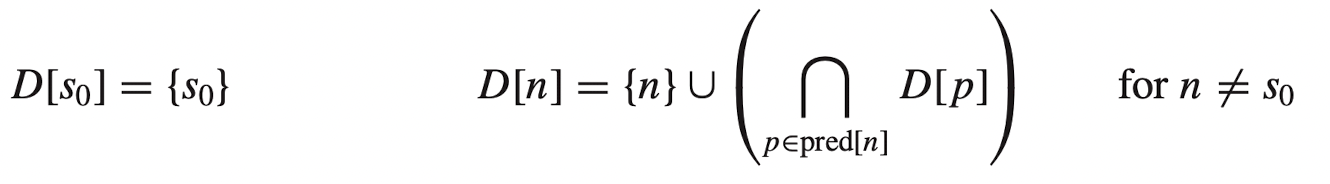
image-20221231125135249

对于给定的一个点n, 其中有p1, p2.....作为其前驱节点, D[i]表示的是i的必经结点的集合.在进行计算时可以通过类似于拓扑排序或者dfs的模式进行递归求解.

直接必经结点

定理: 如果d、e都是n的必经结点, 要么是d为e的必经结点, 要么e是d的必经结点.

直接必经结点(idom)的性质如下:

  • idom(n) != n
  • 是n的必经结点.
  • 不是其他必经结点的必经结点.

除了S0外, 所有其他结点都至少有一个除自己之外的必经结点, 因此除了S0外, 所有其他结点都恰好有一个直接必经结点.可以将概念理解成距离结点n最近的必经结点.

关于必经结点树, 直将每个结点的直接必经结点画出来就好了.

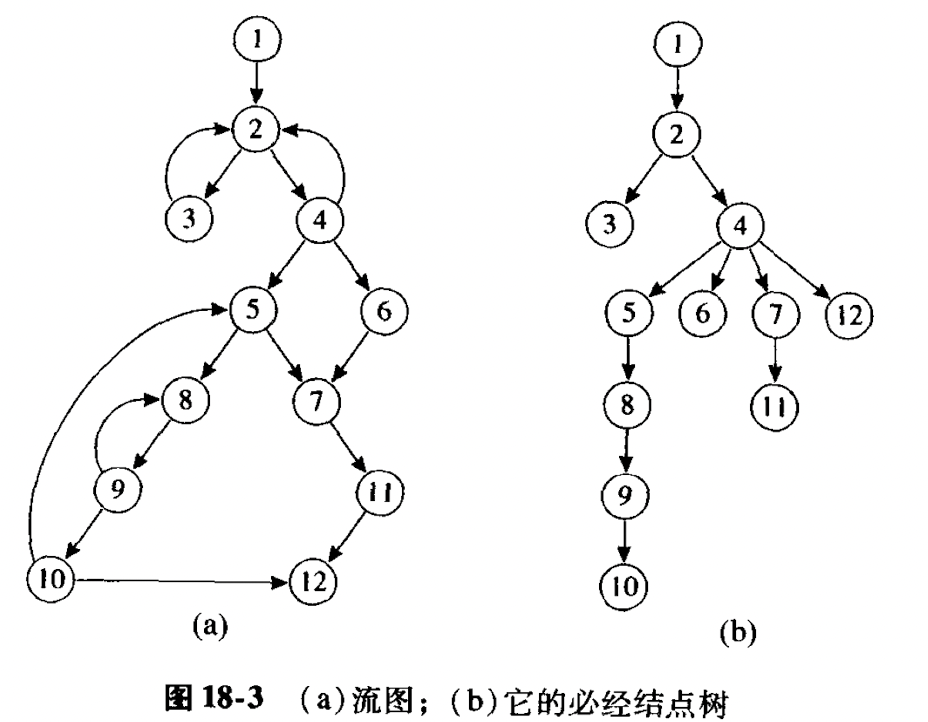
image-20221231125744494

循环

自然循环: 集合中的任何结点x, 其必经结点都有h, 并且有一个从x到n不包含h的路径.

最内层循环往往是最值得优化的, 但是对于共享header结点的循环来说, 难以确定哪一个才是最内层循环, 对此的处理方式有将这些同一个header的循环合并, 但是合并之后就不一定是自然循环了.

嵌套循环: A和B是两个循环体,两者不共享header结点, 但是b(B的header结点)在A中,那么B结点也就是A结点的真子集.B就是A的内循环.

一个循环嵌套树如下所示:

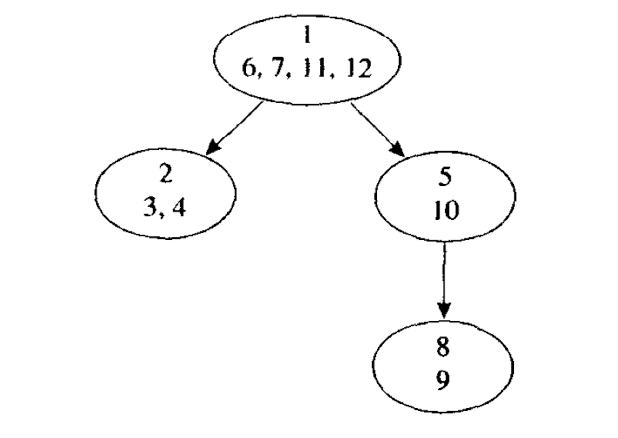
image-20221231131830163

循环前置结点

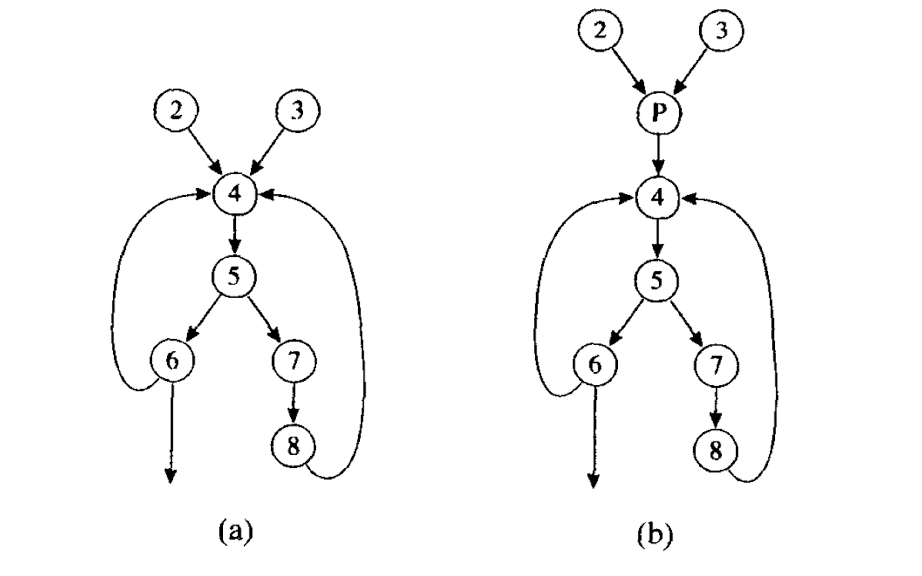
很多循环优化都需要将一些语句插入到即将进入到循环体之前要执行的位置.比如说循环不变量外提.因此需要一个循环前置结点.

加入循环前置结点之后, 循环内到header的结点仍然指向header, 但是循环外部的结点指向header的路径都被重定向到了header.

image-20221231133110940

2) 循环不变量计算

首先需要确定的是, 对于一个d: t <- a1 op a2是否是循环不变量的条件(满足其中之一即可)是:

  • a1和a2都是常数.
  • 所有到达的d的ai定值都在循环之外.
  • a1和a2中只有一个定值到达d, 并且该定值是循环不变量.

其中简要说明其方法为:

  • 找出所有操作数是常数或者循环外定值的语句.
  • 重复地寻找其操作数都为循环不变量的定值.

确定循环不变量之后, 需要考虑的是外提.然而外提又是结果不会正确.比如说下面的这几个例子:

image-20221231134307261

因此考虑还增加一些限制条件:

  • d是所有该循环出口结点的必经结点: 也就是说t在循环出口结点, t是活跃的.
  • 在循环体中t只有一个定值.
  • t不属于循环前置结点的出口活跃集合.

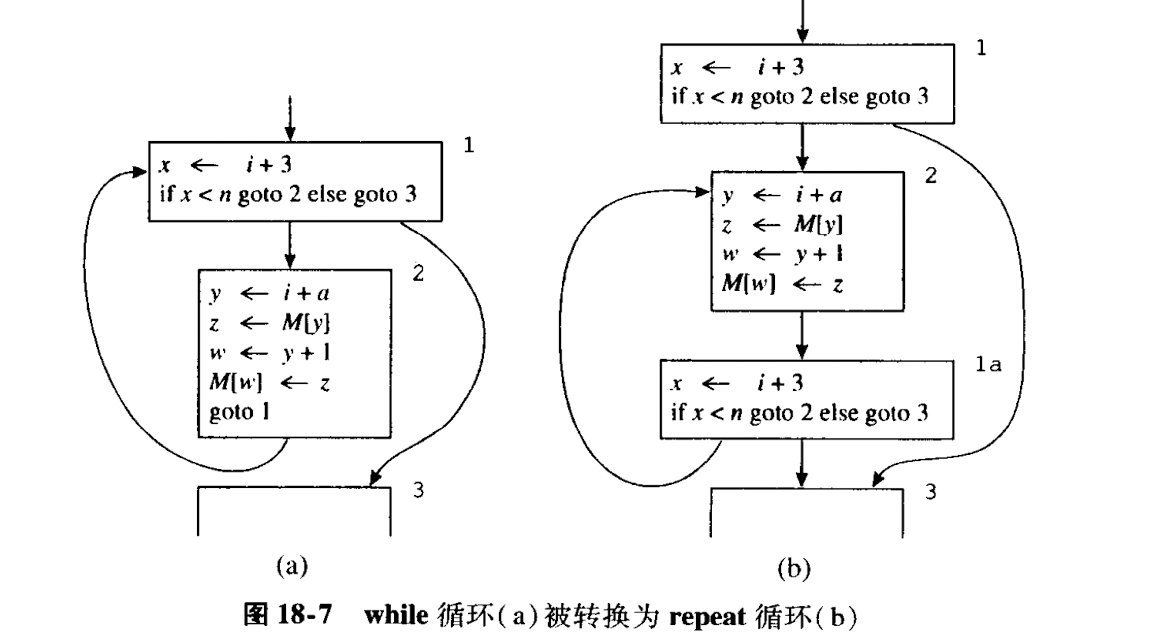
image-20221231134903709

5. 部分冗余消除

这种优化的目的在于尽量减少表达式求值的次数.比如说可以通过移动x+y这种表达式的求值的位置, 在必要时将求值结果保存在临时变量中.由于需要寻找适当的位置对表达式进行求值, 因此需要借助数据流分析技术.

关于对部分冗余的理解, 指的是冗余只存在于部分路径而非全部路径中(其实之前学到的公共子表达式和循环不变代码移动都是其中的特例).

懒惰代码移动问题

我们所期望的部分冗余消除算法优化应该能达到以下的目的:

  • 所有不复制代码就可以消除的表达式冗余计算都被消除了.
  • 优化之后的程序不会执行原本不执行的计算.
  • 尽可能将表达式的计算时刻延后(声明周期往往缩短, 涉及到的路径减少).

懒惰代码移动就是以第三点为目的的优化方式.

6. 寄存器分配与指派

在生成的IR代码中, 其中假定有无限数量的寄存器. 寄存器分配的任务在于将大量的临时变量分配到符合目标机器的有限的寄存器之中.其前提往往需要使用到通过数据流分析所得来的冲突图, 在冲突图中, 每个结点代表了IR中的一个临时变量, 存在边的一对结点表示的是不能分配同一个寄存器的变量.

如果想要通过冲突图找出一个寄存器分配方案, 需要做的就是运行图着色算法, 追求尽可能少的颜色, 并且存在边的结点之间不可以使用相同的颜色.

1) 基本概念

图着色算法本身是一个NP完全问题, 但在实际开发中可以通过一种线性时间的方法.其过程分为四步骤:

  • 通过数据流分析构造冲突图.需要借助活跃分析(确切地说是live range, 对于live range发生重叠的变量来说, 需要在冲突图中构造出边).
  • 简化启发式地对图着色:
    • 假设图G有一个结点m, 其邻居点数少于K, K是机器寄存器的个数.
    • 设G‘为从G中去除了m的子图, 如果G’可以用K色着色, 那么G也可以.(因为m的邻居少于K, 这些邻居最多用K-1种颜色).
    • 简而言之, 重复地删除度数少于K的结点(将其入栈), 每减少掉一个同时也就减少了其他节点的度数.
  • 对于某一个度数大于等于K的结点, 需要考虑溢出.此时考虑在图中选择一个结点, 将其放在内存中, 不再对其分配寄存器,同时也将其入栈.
  • 将颜色指派给图中的结点. 此时冲突图是一个空的状态, 这时将栈顶的结点不断地加入到原图中, 每加一个结点就对其着色.

总体来说, 这里需要区分简化版:每次只是选择度数<n的结点, 将其从图中移除后入栈, 迭代直到图为空为止.之后分配颜色, 从栈中逐个弹出, 插入图中原本的位置, 并同时分配颜色, 直到栈空.

2) 合并

如果在冲突图中, 一个传送(内存move)指令的源操作数和目的操作数对应的结点不存在边, 可以删除该传送指令, 可以合并成新的结点.

但是由于合并两个结点之后, 导致冲突图发生变化, 因此可能导致原本可K着色的图成了不可着色的, 如何应对这种问题呢, 需要为可合并结点增加额外的条件:

  • Briggs: 如果合并后的结点仍然度数少于K, 那么可以合并.
  • George:

因此考虑了合并之后的图着色算法流程如下:

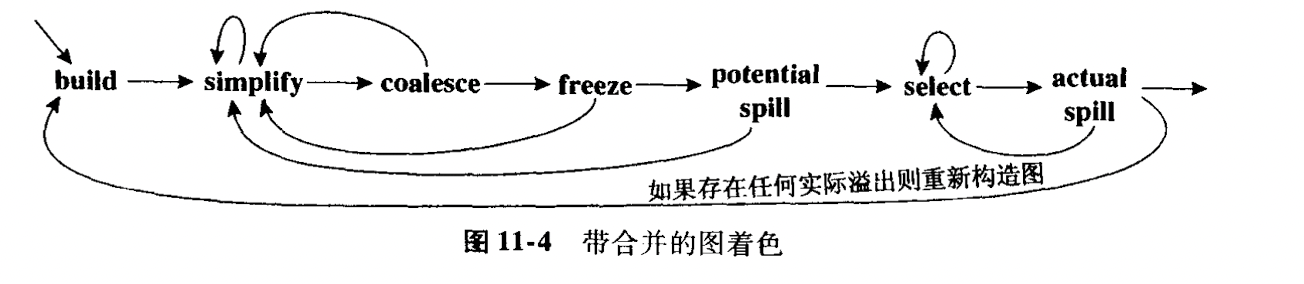
image-20230104231207297

这里总结一下带有合并的图着色算法:

  • 构造, 将结点分为传送有关和传送无关的.
  • 简化, 每次将低于K度数的结点移除,并入栈.
  • 合并, 对简化图进行合并.
  • 冻结, 如果简化和合并都不能进行, 寻找一个度数较低的传送相关的结点, 冻结该指令所关联的传输指令.
  • 移除, 如果没有低度数结点, 选择一个可能移除的高度数结点并将其压栈.
  • 选择, 弹出栈, 同时指派颜色.

3) 预着色的结点

机器寄存器是需要进行预着色的.

4) 图着色相关实现

虎书中中对于对于冲突图的实现建议是, 同时使用邻接表和临接矩阵实现, 因为前者对于获取某结点的所有相邻结点比较方便, 而后者对于判断某两个结点(比如说X和Y)是否相邻比较方便.

虎书中给出一个递归的伪代码:

image-20230104223949762

Reference

编译工程9：中间代码生成

代码优化与LLVM IR pass

编译器算法之寄存器分配